PS:本文中的log等同于我们国内的ln
sigmoid函数
之前那一文中提到了一般的梯度上升的公式推导,但是在《机器学习实战》一书中,实现的是分类方法,因此,虽然最终的结果相似,但是其实本质有很大的不同。
一般来讲我们把实物分成两类,因此我们需要将结果映射到两个结果(是或非),因为一般的阶跃函数在求导之类的问题上会变得相当复杂,因此我们用一个更加圆滑的sigmoid函数来映射,所有输入到这个函数的实数都会被转化到0-1之间,它的公式为 $ g(z)=\frac{1}{1+e^{-z}} $
同时它对应的图像如图所示: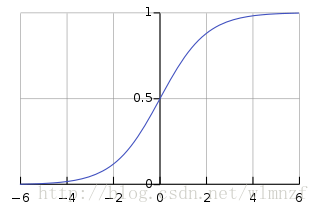
于是我们可以将得到的结果进行四舍五入,分类成0或1
Logistic 回归
这里的意思是,将我们的分类边界线作模型,进行拟合,并以此来分类。
我们假设经过sigmoid函数处理过的结果为 $h_{\Theta}(x)$ ,因为是在0-1之间,因此可以看做是概率,另外,我们可以假设,分类到0或者1的概率。
$$
P(y=1|x;\theta)=h_{\theta}(x) \\
P(y=0|x;\theta)=1-h_{\theta}(x) \tag{1}
$$
将以上两个概率公式整合一下成为一个概率公式,
$$
p(y|x;\theta)=(h_\theta(x))^y(1-h_\theta(x))^{1-y} \tag{2} \\
$$
梯度上升解决回归问题
1. 最大似然估计
这里我们使用最大似然估计法,这个在大学的高等数学中应该都有学习过,就不在赘述。这里假设我们有m个训练集。
$$
L( \theta )=\prod_{i=1}^{m}p(y^{(i)}|x^{(i)};\theta)=\prod_{i=1}^{m}(h_\theta(x^{(i)}))^{y^{(i)}}(1-h_\theta(x^{(i)}))^{1-{y^{(i)}}} \tag{3}
$$
为了求导方便,我们一般会将似然函数L加上log函数,因为log函数是递增函数,因此不影响似然函数求最值。
这里会用到一个log函数的性质 $log a^b=b log a$ ,推导得:
$$
l(\theta)=logL(\theta)=\sum_{i=1}^my^{(i)}logh(x^{(i)})+(1-y^{(i)})log(1-h(x^{(i)})) \tag{4}
$$
将l函数对$\theta$求导
$$
\frac{\partial}{\partial\theta_j }l(\theta)=(y\frac{1}{h_\theta (x)}-(1-y)\frac{1}{1-h_\theta (x)})\frac{\partial}{\partial\theta_j}h_\theta x \tag{5}
$$
2. sigmoid函数求导
$$
\begin{equation}
\begin{split}
&h’(x)=\frac{d}{dx}\frac{1}{1+e^{-x}}\\
&=\frac{1}{(1+e^{-x})^2} (e^{-x})\\
&=\frac{1}{(1+e^{-x})}(1-\frac{1}{(1+e^{-x})})\\
&=h(x)(1-h(x))
\end{split}
\end{equation} \tag{6}
$$
3. 似然估计后续
从上一篇文章,或者从《机器学习实战》chapter5 中可得sigmoid函数h(x)的输入函数是$w=\theta^Tx$,将其代入公式(4),得到
$$
\begin{equation}
\begin{split}
&l’(\theta)=(y\frac{1}{h(\theta^Tx)}-(1-y)\frac{1}{1-h{(\theta^Tx)}}) \frac{\partial}{\partial\theta_j}h(\theta^Tx)\\
&=(\frac{1}{h(\theta^Tx)}-(1-y)\frac{1}{1-h(\theta^Tx)})h(\theta^Tx)(1-h(\theta^Tx)\frac{\partial}{\partial_j}\theta^Tx)\\
&=(y(1-h(\theta^Tx))-(1-y)h(\theta^T x))x_j\\
&=(y-h_\theta(x))x_j
\end{split}
\end{equation} \tag{7}
$$
William
会打代码的扫地王大爷
wlmnzf
中科院信工所
IIE
CAS
csuncle
丁洁的男朋友
丁洁的人
王立敏