梅森旋转算法安全性分析及改进

Posted on | In


梅森旋转算法安全性分析及改进
======================

王立敏1,丁洁2

1中国科学院信息工程研究所 第五实验室 北京 中国100093

2中国科学院信息工程研究所 第五实验室 北京 中国100093

摘要
梅森旋转算法是目前最流行的伪随机数发生器算法之一。梅森旋转算法存在许多缺点，例如当生成的伪随机数数量庞大时可预测以及无法通过部分统计测试。为了更好地深入了解和分析梅森旋转算法的安全性，本文将使用NIST
800-22文档中提到的统计测试等方法来对其生成的伪随机数进行静态的质量评估，并通过伪代码对该算法进行理论安全分析。由于梅森旋转算法生成伪随机数的速度十分快，而且开发者和研究人员们已经开发了许多梅森旋转算法的改进版本，甚至密码学安全的版本，因此当需要伪随机数时，选用梅森旋转算法作为伪随机数生成器是合理的。

关键词 梅森旋转算法，MT19937标准，统计测试，安全性分析

The Analysis And Improvement Of Mersenne Twister

Wang Limin1, Ding Jie2

1Institute of Information Engineering, Chinese Academy of Sciences, Beijing 100093, China


2Institute of Information Engineering, Chinese Academy of Sciences, Beijing 100093, China

Abstract Mersenne Twister is one of the most useful pseudo random number generator algorithms. There are many shortcomings in Mersenne Twister. For example, it would be predictable and could not pass some of statistical tests when the algorithm generates plenty of pseudo random number generator algorithms. To analyze the security of algorithm, the statistical tests mentioned in NIST 800-22 would be used to evaluate the quality of Mersenne Twister and the pseudocode would be used to analyze the security of the algorithm. Mersenne Twister is very fast, and the developers and researchers have developed the improved versions of this algorithm, even the cryptographically secure version. For these reasons, choosing Mersenne Twister as the alternative pseudo random number generator is reasonable.

Key words Mersenne Twister, MT19937, statistical test, the analysis of security

1 前言

        随机数在许多领域中都有着大量应用，例如密码学，游戏，数学统计。随机数主要分两类，分别是确定性随机数和非确定性随机数。非确定性随机数也可称为真随机数（True Random Number Generator, TRNG），主要来源于不可预测的物理或者化学熵源，例如电路噪声。真随机数发生器产生的随机数质量十分高，是最理想的随机数来源，但是由于产生的速度太慢，无法满足目前的信息的传输速度，因此目前确定性随机数依然被广泛使用。确定性随机数发生器也称作伪随机数发生器（Pseudorandom Number Generator，PRNG）,它一般是一个随机数生成算法，由于算法是固定的，因此生成的随机数存在许多诸如可预测，质量不高的缺点。因此在使用一个伪随机数发生器之前对其进行评估是十分有必要的。

        梅森旋转是目前应用十分广泛的伪随机数生成器算法之一，已经集成在C++等编程语言的标准库中。梅森旋转生成的随机数能通过常见的静态统计测试，并且生成速度十分快，但是它依然存在许多缺点，例如当随机数数量足够时可预测。本文主要对该方法进行质量评估和安全性分析，并且提出一些改进意见。

2 梅森旋转

        MT19937以及MT19937-64标准分别实现了梅森旋转的32位以及64位算法，由于这两者只是参数不同，因此为方便起见，只实现和讨论MT19937标准。MT19937标准采用的梅森素数为219937
-1，因此它可生成的随机数范围为[0, 219937 -1]。

        梅森旋转算法实际使用的是旋转的广义反馈移位寄存器（Twisted Generalized Feedback Shift Register,GFSR）[2]，它主要分初始化，旋转生成随机数以及Xorshift后期处理三个步骤。由于MT19937的梅森算法中生成的随机数为32位，因此算法需要624个32位长的状态。在初始化阶段，算法的工作是将我们获得的随机种子经处理填充到所有的624个状态中

算法1：初始化
输入: 一个随机种子seed 
1
2
3
4
5
6
mt[0] = seed 
a=1812433253  
FOR i FROM 1 TO 623 
  { 
     mt[i] = f * (mt[i-1] XOR (mt[i-1] >> 30)) + i    
  }

        MT19937规定了算法1中的f值为1812433253 ，算法将输入的随机种子赋值给第0个状态，剩余的623个状态则用前一状态值的一系列操作进行赋值更新。当执行完这一算法后，全部的624个状态已经填充完毕，之后梅森算法便可以不断地生成伪随机数。

算法2：旋转生成随机数 
1
2
3
4
5
6
7
8
9
10
11
12
13
lower_mask = (1 << 31) - 1, 
upper_mask = (1 << 31)
a = 0x9908B0DF
FOR i FROM 0 TO 623
  {
    x = (mt[i] AND upper_mask) +(mt[(i+1) MOD 32] AND lower_mask)
    xA = x >> 1
    IF (x MOD 2) != 0
    {
      xA = xA XOR a
    }
    mt[i] = mt[(i + 397) MOD 624] XOR xA
 }

        MT19937标准中定义a的值为0x9908B0DF，如算2所示，这部分是进行旋转操作。每生成624个伪随机数后，将执行一次算法2，重新更新624个状态，为生成下一批624个伪随机数做准备。

算法3:Xorshift后期处理
输出：生成的伪随机数y 
1
2
3
4
5
6
7
b = 0x9d2c5680 
c = 0xefc60000 
y = mt[i] 
y = y XOR (y >> 11) 
y = y XOR ((y << 7) AND b) 
y = y XOR ((y << 15) AND c) 
y = y XOR (y >> 18)

每个状态都需要经过Xorshift操作[3]以后才能成为最终输出的伪随机数，由于其中几乎都是移位，因此对CPU来说是十分快的。

3 伪随机数发生器的评估

正如前言部分所述，伪随机数发生器的评估是十分有必要的。伪随机数的质量和安全性一般有如下4个评判标准:

  1. 随机数应该有很好的统计属性。例如各态遍历性

  2. 不能根据随机数的子序列合理推出其之前或者之后的随机数序列。并且子序列不能提高推出其之前和之后的伪随机序列的可能性。

  3. 不能根据内部状态合理推出其之前的内部状态。同样的也不能通过内部状态提高推出其之前的内部状态的可能性。

  4. 不能根据内部状态合理推出其之后的内部状态。也不能通过内部状态提高推出其之后的内部状态。

梅森旋转伪随机数的质量评估

4.1 NIST 800-22测试

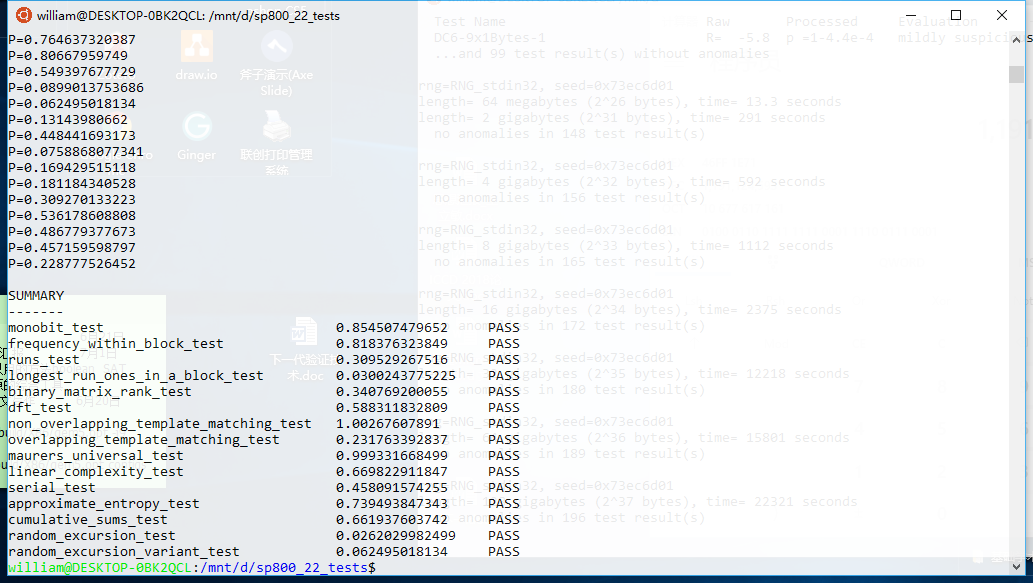
图1 NIST 800-22随机数测试

图1 NIST 800-22随机数测试

        NIST 800-22文档中提到了许多静态测试[4]，并且提供了测试程序NIST STS-2.1.2。David Johnston认为STS程序存在许多问题，例如经常奔溃，并且给出错误的测试结果，因此他修正了这些错误，并且给出了修正后的程序[5]。本测试采用了该自动化测试程序，在Summary一栏中左侧为测试名称，右侧为测试的统计参数P值，如图可见该梅森旋转算法可以通过文档中提到的所有静态测试。

4.2 PractRand测试

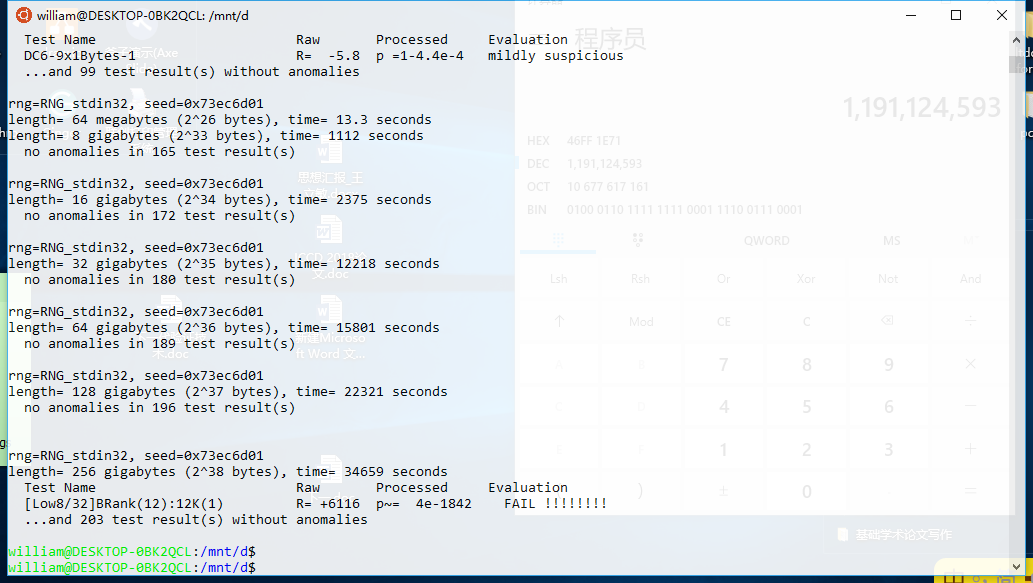
图2 PractRand随机数测试

图2 PractRand随机数测试

        PractRand也是目前常采用的测试程序。由图2所示，我们可以看到当随机数输出大小为128G时可以满足常见的静态统计测试，但是当输出随机数的数量达到256G时，BRANK测试无法通过。

4.3 安全性分析

        第三部分的算法3将状态进行移位和亦或，最终输出为伪随机数，但是这一过程是可逆的。逆过程的具体证明和分析方法可参看oupo和plusletool的博客[6,7]。

算法4: 算法3的逆过程
输出：梅森旋转的中间状态value 
1
2
3
4
5
6
7
8
9
10
11
value = y 
value = value XOR (value >> 18)
value = value XOR (value << 15) AND 0xefc60000
value = value 
       XOR ((value << 7) & 0x9d2c5680) 
       XOR ((value << 14) & 0x94284000) 
       XOR ((value << 21) & 0x14200000) 
       XOR ((value << 28) & 0x10000000) 
value =value 
       XOR (value >> 11) 
       XOR (value >> 22)

        算法4描述了如何由伪随机数逆向恢复到梅森旋转算法的状态，因此若我们有624个梅森旋转算法生成的伪随机数，则我们可以由算法4恢复得到624个中间状态。再通过算法2和算法3即可得到接下来的伪随机数了。

        但是由算法2可知，在进行旋转的时候，需要用到第i个状态，第i+1个状态以及第i+397个状态。因此如果敌手所得到的伪随机数量或者状态不足，则不能恢复所有的624个状态，便也不能继续预测接下来的伪随机数。而且算法2中的旋转操作会直接覆盖之前的内部状态，而且算法中跟mask进行与操作以及右移操作使得它无法再逆向推导出之前的状态，因此所幸的是即使敌手获取到足够量的伪随机数，也无法推出之前的伪随机数。

        梅森旋转算法可以满足常见应用的随机数需求，但是对于加密过程中所需的伪随机数，还是需要使用密码学安全的伪随机数（Cryptographically
Secure Pseudo-Random Number
Generator，CSPRNG），例如改进版的梅森旋转算法CryptMT。

5 梅森旋转的改进方案

5.1 Hash输出

        由于梅森旋转算法可逆，我们可以通过泄露的伪随机数逆向推算出其内部状态，因此若将最终输出再进行Hash处理，如图3所示，即可使其生成的伪随机数不可逆，这样便可一定程度上提高梅森旋转算法的安全性。

        Hash算法不可逆，并且可以被用来生成伪随机数[8]，生成的随机数也具有很好的安全性。此外，SHA-3之所以拥有安全，不可逆等良好的特性，是因为采用了海绵结构，而且目前已经存在基于海绵结构的伪随机数生成器了[9,10]。综上所述，Hash算法可以用于生成质量较高的伪随机数，而且不可逆，若想要更灵活方便地移植使用，则也可以直接使用海绵结构。因此改进方案中采用Hash对梅森算法的输出做最后的处理使其不可逆是合理的。

图3 经过Hash的梅森算法

图3 经过Hash的梅森算法

5.2 间隔输出

        由算法2可知，当梅森算法更新当前第i个状态时必须要用到第i+1个状态以及第i+397个状态。因此如图4所示假设将这些状态每隔一个进行处理输出为伪随机数，则即使敌手获取到大量的间隔伪随机数，并且将他们逆向恢复为算法的内部状态，也无法得到完整的624个状态。若没有完整的624个状态，则也无法继续预测生成接下去的伪随机数。

图4 间隔输出的梅森算法

图4 间隔输出的梅森算法

6 结论

        根据第3部分所描述的4个评估标准可知梅森旋转算法并不完美。它依然无法通过其中的小部分统计测试，例如当生成的伪随机数达到256G时，无法通过BRANK测试。当敌手可以获得超过624个伪随机数时，可以通过逆向推导出其内部状态来预测其接下来生成的伪随机数。不过所幸的是由于其更新内部状态时的操作不可逆，使得它无法推导出已经生成过的伪随机数。对于第四个评估标准，事实上包括梅森旋转在内的确定性的伪随机数发生器都无法满足，因为算法固定，因此只要获取到内部状态，就一定可以推算出之后的伪随机数。

        梅森旋转算法虽然存在许多的缺点，比如当获取到的伪随机数数量足够多时是可以预测的，并且无法通过一些静态统计测试。但是由于它的许多操作都是基于移位的，因此速度更快一些。并且近些年来，许多开发者和研究人员都为改进梅森旋转算法做出了许多努力，诞生了许多更优秀的基于梅森旋转算法的随机数生成器，例如CryptMT，MTGP。

        因此在通用的软件上使用改进版的梅森旋转算法，以及在加密时使用密码学安全的梅森旋转算法（CryptMT）是十分合理的。

代码请看这里

参考文献

[1] 徐恒. 确定性随机数产生器安全性分析及改进[D]. 上海交通大学, 2009.

[2] MATSUMOTO M, KURITA Y. Twisted GFSR generators[J]. ACM Transactions on
Modeling and Computer Simulation, 1992, 2(3): 179–194.

[3] MARSAGLIA G, OTHERS. Xorshift rngs[J]. Journal of Statistical Software,
2003, 8(14): 1–6.

[4] NIST S. 800-22[J]. A Statistical Test Suite for Random and Pseudorandom
Number Generators for Cryptographic Applications, 2000, 120.

[5] JOHNSTON D. sp800_22_tests: A python implementation of the SP800-22 Rev 1a
PRNG test suite[M]. 2018.

[6] PLUSLETOOL. メルセンヌ・ツイスタのtemperingの逆関数に関する考察[EB/OL]. Plus
Le Blog, 1414154296. (1414154296)[2018-07-15].
http://plusletool.hatenablog.jp/entry/2014/10/24/213816.

[7] 2014-10-16[EB/OL]. oupoの日記, [2018-07-15].
http://d.hatena.ne.jp/oupo/20141016.

[8] BOLDYREVA A, KUMAR V. A New Pseudorandom Generator from Collision-Resistant
Hash Functions[G]//DUNKELMAN O. Topics in Cryptology – CT-RSA 2012. Berlin,
Heidelberg: Springer Berlin Heidelberg, 2012, 7178: 187–202.

[9] BERTONI G, DAEMEN J, PEETERS M等. Sponge-Based Pseudo-Random Number
Generators[G]//MANGARD S, STANDAERT F-X. Cryptographic Hardware and Embedded
Systems, CHES 2010. Berlin, Heidelberg: Springer Berlin Heidelberg, 2010, 6225:
33–47.

[10] BERTONI G, DAEMEN J, PEETERS M等. Duplexing the Sponge: Single-Pass
Authenticated Encryption and Other Applications[G]//MIRI A, VAUDENAY S. Selected
Areas in Cryptography

William Wang wechat
Welcome！
I'm happy it's useful to you!