一、本文的意义
因为谷歌官方其实已经写了MNIST入门和深入两篇教程了，那我写这些文章又是为什么呢，只是抄袭？那倒并不是，更准确的说应该是笔记吧，然后用更通俗的语言来解释，并且补充更多，官方文章中没有详细展开的一些知识点，不过建议与官方文章结合着阅读。
另外是代码部分的改动，官方的demo只提供了验证精确度，我将它改造成了能输入并预测输出结果的代码也就是说是一个从准备待测图片到最终是别的一个完整demo
中文版本：MNIST机器学习入门
http://wiki.jikexueyuan.com/project/tensorflow-zh/tutorials/mnist_beginners.html
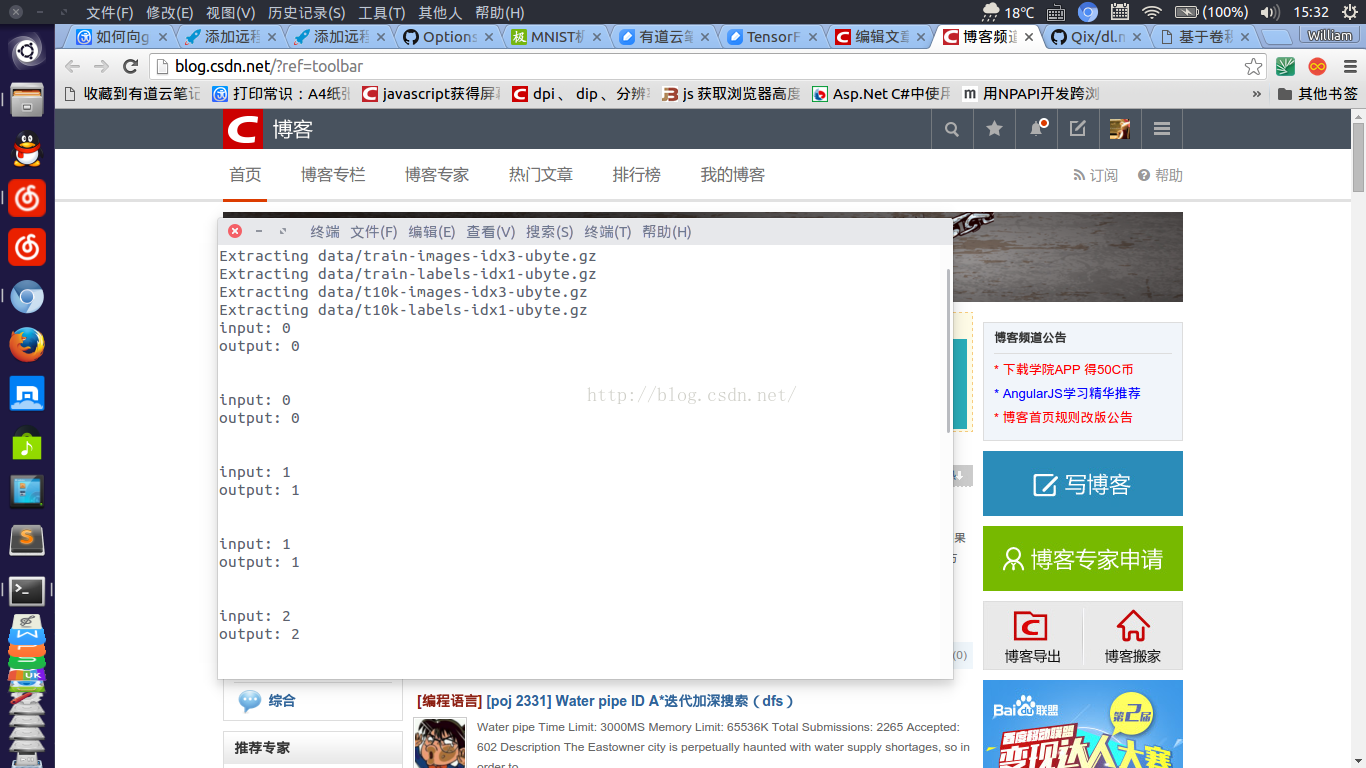
需要识别的图片放到test_num里，然后运行mnist_softmax.py就好了
demo截图如下，会将放进去的图片预测，然后输出结果，代码说明请看github的readme（最底下）
二、MNIST简介
这个MNIST数据库是一个手写数字的数据库，它提供了六万的训练集和一万的测试集。
它的图片是被规范处理过的，是一张被放在中间部位的28px*28px的灰度图
总共4个文件:\
train-images-idx3-ubyte: training set images \
train-labels-idx1-ubyte: training set labels \
t10k-images-idx3-ubyte: test set images \
t10k-labels-idx1-ubyte: test set labels\
图片都被转成二进制放到了文件里面，
所以，每一个文件头部几个字节都记录着这些图片的信息，然后才是储存的图片信息
TRAINING SET LABEL FILE (train-labels-idx1-ubyte):
1 | 0000 32 bit integer 0x00000801(2049) magic number (MSB first) |
The labels values are 0 to 9.
TRAINING SET IMAGE FILE (train-images-idx3-ubyte):
1 | 0000 32 bit integer 0x00000803(2051) magic number |
每个像素被转成了0-255,0代表着白色，255代表着黑色。
TEST SET LABEL FILE (t10k-labels-idx1-ubyte):
1 | 0000 32 bit integer 0x00000801(2049) magic number (MSB first) |
The labels values are 0 to 9.
TEST SET IMAGE FILE (t10k-images-idx3-ubyte):
1 | [offset] [type] [value] [description] |
每个像素被转成了0-255,0代表着白色，255代表着黑色。
三、tensorflow手写数字识别的大致步骤
- 将要识别的图片转为灰度图，并且转化为28*28矩阵（单通道，每个像素范围0-255，0为黑色，255为白色，这一点与MNIST中的正好相反）
- 将28*28的矩阵转换成1维矩阵（也就是把第2,3,4,5….行矩阵纷纷接入到第一行的后面）
- 用一个1*10的向量代表标签，也就是这个数字到底是几，举个例子e数字1对应的矩阵就是[0,1,0,0,0,0,0,0,0,0]
- softmax回归预测图片是哪个数字的概率
- 用交叉熵和梯度下降法训练参数
四、过程讲解
4.1 准备要识别的图片
这个部分其实是比较重要的，因为如果处理不得当可能并不一定会有很好的结果，所以按照mnist的标准规范需要将待测图片转为28×28且文字居中的灰度图（其实彩色的也可以，不过就是最后代码需要改一下），目前介绍两种获得待测图片的方法：
- 自己用ps或者真的手写一些数字
- 将MNIST数据库中的二进制转化成图片，然后用来做测试
ps:图片解析 点击进入
4.2 将待测图片转换为矩阵
如图所示，根据黑色部分的浓淡将其转化成微一个浮点数的数组，（白色0,黑色1）
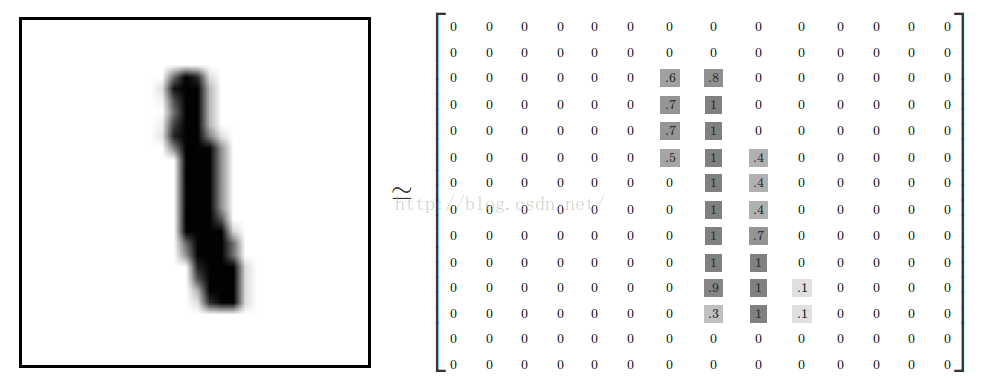
看到这里，如果你跟我一样不熟悉python，是不是开始方了，没事，其实python很厉害，自带的PIL图片库一句话就可以搞定
1 | img=array(Image.open(filename)) //打开然后就被numpy转化了 |
如果是彩色的图片，则需要先将它这样子转换一下（我当初并不知道可以转化，傻不垃圾地自己写了一个转化，所以python还是好好学习啊）1
Lim = img=array(im.convert("L"))
4.3将矩阵转化为一维矩阵,以及标签的介绍
转化为一维的矩阵其实并不难，用python的reshape就能搞定，还是要讲一下标签的表示方法，这个曾经令队友疑惑不久，直到我把这个数组打印出来
4.3.1标签的来历–有监督学习 和 无监督学习
监督学习：利用一组已知类别的样本调整分类器的参数，使其达到所要求性能的过程，也称为监督训练或有教师学习
举个例子，MNIST自带了训练图片和训练标签，每张图片都有一个对应的标签，比如这张图片是1，标签也就是1,用他们训练程序，之后程序也就能识别测试集中的图片了，比如给定一张2的图片，它能预测出他是2
无监督学习：其中很重要的一类叫聚类
举个例子，如果MNIST中只有训练图片，没有标签，我们的程序能够根据图片的不同特征，将他们分类，但是并不知道他们具体是几，这个其实就是“聚类”
4.3.2 标签的表示
在这里标签的表示方式有些特殊，它也是使用了一个一维数组，而不是单纯的数字，上面也说了，他是一个一位数组，0表示方法[1,0,0,0,0,0,0,0,0,0],1表示[0,1,0,0,0,0,0,0,0,0],………， 主要原因其实是这样的，因为softmax回归处理后会生成一个1*10的数组，数组[0,0]的数字表示预测的这张图片是0的概率，[0,1]则表示这张图片表示是1的概率……以此类推，这个数组表示的就是这张图片是哪个数字的概率（已经归一化），因此，实际上，概率最大的那个数字就是我们所预测的值。两者对应来看，标准的标签就是表示图片对应数字的概率为100%，而表示其它数字的概率为0，举个例子，0表示[1,0,0,0,0,0,0,0,0,0]，可以理解为它表示0的概率为1，而表示别的数字的概率为0.
4.4 softmax回归
这是一个分类器，可以认为是Logistic回归的扩展，Logistic大家应该都听说过，就是生物学上的S型曲线，它只能分两类，用0和1表示，这个用来表示答题对错之类只有两种状态的问题时足够了，但是像这里的MNIST要把它分成10类，就必须用softmax来进行分类了。
P(y=0)=p0,P(y=1)=p1,p(y=2)=p2……P(y=9)=p9.这些表示预测为数字i的概率，（跟上面标签的格式正好对应起来了）,它们的和为1，即 ∑(pi)=1。
tensorflow实现了这个函数，我们直接调用这个softmax函数即可，对于原理，可以参考下面的引文，这里只说一下我们这个MNIST demo要用softmax做什么。
（注：每一个神经元都可以接收来自网络中其他神经元的一个或多个输入信号，神经元与神经元之间都对应着连接权值，所有的输入加权和决定该神经元是处于激活还是抑制状态。感知器网络的输出只能取值0或1，不具备可导性。而基于敏感度的训练算法要求其输出函数必须处处可导，于是引入了常见的S型可导函数，即在每个神经元的输出之前先经过S型激活函数的处理。）
4.5 交叉熵
通俗一点就是，方差大家都知道吧，用它可以衡量预测值和实际值的相差程度，交叉熵其实也是一样的作用，那为什么不用方差呢，因为看sigmoid函数的图像就会发现，它的两侧几乎就是平的，导致它的方差在大部分情况下很小，这样在训练参数的时候收敛地就会很慢，交叉熵就是用来解决这个问题的，它的公式是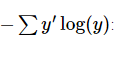 
,其中，y 是我们预测的概率分布, y’ 是实际的分布。
4.6 梯度下降
上面那步也说了，有个交叉熵，根据大伙对方差的理解，值越小，自然就越好，因此我们也要训练使得交叉熵最小的参数，这里梯度下降法就派上用场了，这个解释见上一篇系列文章吧，什么叫训练参数呢，可以想象一下，我们先用实际的值在二位坐标上画一条线，然后我们希望我们预测出来的那些值要尽可能地贴近这条线，我们假设生成我们这条线的公式ax+ax^2+bx^3+…..，我们需要生成这些系数，要求得这些系数，我们就需要各种点代入，然后才能求出，所以其实训练参数跟求参数是个类似的过程。
4.7 预测
训练结束以后我们就可以用这个模型去预测新的图片了，就像我们已经求出来了方程，以后只要随意输入一个x，就能求出对应的y。
5 代码
https://github.com/wlmnzf/tensorflow-train/tree/master/mnist
6 参考文章
http://blog.csdn.net/acdreamers/article/details/44663305 softmax回归
http://wiki.jikexueyuan.com/project/tensorflow-zh/tutorials/mnist_beginners.html MNIST学习入门
http://blog.csdn.net/u012162613/article/details/44239919 交叉熵代价函数
