前言
本来对数学没什么感觉的,但是停摆了一年复习考研,于是开始对数学有些感觉了,之前看到《机器学习实战》中第五章中梯度上升法,使用了一个它所谓的十分简单的推导,一直好奇怎么个简单法,于是重新学习机器学习的相关算法,这次将主推数学推导。
有监督回归算法
在机器学习中,多元线性回归模型是经常使用的模型,比如在吴恩达《斯坦福机器学习》中的例子,我们需要根据已有的房价信息预测当前房子的房价,于是我们收集到一些房价数据。
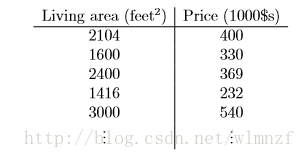
再将它们画在二维坐标上,它们就以离散的点分布在平面上,如下所示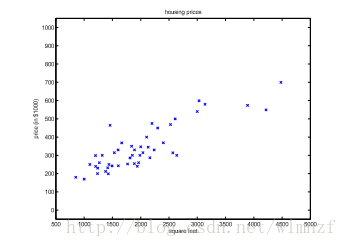
我们希望能根据这些已知的点来预测我们想知道的房子的房价,因此我们需要找到一条规律,也就是一条大致经过这些点的线性模型,在数学上我们通常称之为拟合,而这个拟合的过程,我们称之为回归。
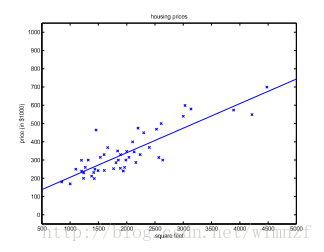
假设我们建立的模型是一元一次的,将得到这样的拟合结果,于是我们可以x轴上的房屋面积,找到对应的房屋价格。
有监督的学习算法,可以理解成我们训练模型的时候每一个输入都是有标准答案的,我们通过预测值跟标准答案的比对,不断修改模型的参数才能最终实现较好地的拟合结果。
最小二乘法
最小二乘法是我们经常使用的拟合算法,它通过最小化误差的平方和寻找数据的最佳函数匹配。
以我们《机器学习实战》第五章作例子,我们假设的模型为z,于是函数即可设为
$$
\begin{equation}
z=w0+w_1x_1+w2x2+w3x3+….+w_nx_n\\=w_0x_0+w_1x_1+w2x2+w3x3+….+w_nx_n (x0=1) \tag{1}
\end{equation}
$$
这种写法也可以表示为向量的写法:
$$
z=w^Tx=
\begin{bmatrix}
w_0&w_1&…&w_n
\end{bmatrix}
\begin{bmatrix}
x_0\\
x_1\\
…\\
x_n\\
\end{bmatrix} \tag{2}
$$
同样的道理,我们也可以这样子表示
$$
z=x^Tw=
\begin{bmatrix}
x_0&x_1&…&x_n
\end{bmatrix}
\begin{bmatrix}
w_0\\
w_1\\
…\\
w_n\\
\end{bmatrix} \tag{3}
$$
刚才我们也提到了,最小二乘法拟合的原理是最小化误差的平方和,我们将这个平方和称为损失函数,跟我们平时常用的方差类似,当这个损失函数越小,我们的模型就越能跟离散的点匹配起来:
$$
f(w)=\frac{1}{2} \sum_{i=1}^m(z_w( x_i) -y_j )^2 \tag{4}
$$
其中的y表示我们给出的标准的特征 $
\begin{bmatrix}
y_0\\
y_1\\
…\\
y_m\\
\end{bmatrix}
$
因为梯度上升算法是用来计算函数的最大值的,而梯度下降算法则是计算函数最小值的。而我们的损失函数自然是越小越好,我们需要求得一个系数来使得f(w)最小,可是使用梯度上升法是用于求最大值的,因此为了用上梯度上升算法,我们最终应该在f(w)前加上负号。假设:
$$
J(w)=-f(w) \tag{5}
$$
接下来我们开始利用矩阵来推算我们的数学公式,因为原始的公式用来做迭代计算会很不方便,因此我们需要一个等价的公式来让我们的算法更加高效,就例如《机器学习实战》chapter5中的那样。假设我们的输入为X,我们有m组训练数据,每个数据有n个特征。则:
$$
\begin{equation}
X=
\begin{bmatrix}
x_{11}&x_{12}&…&x_{1n}\\
x_{21}&x_{22}&…&x_{2n}\\
…&…&…&…\\
x_{m1}&x_{m2}&…&x_{mn}\
\end{bmatrix}
=
\begin{bmatrix}
x_1^{T}\\
x_2 ^{T}\\
…\\
x_m\\
\end{bmatrix} \tag{6}
\end{equation}
$$
于是通过(3)可以推出
$$
Xw=
\begin{bmatrix}
x_1^T\\
x_2^T\\
…\\
x_m^T\\
\end{bmatrix}
w=
\begin{bmatrix}
x_1^Tw\\
x_2^Tw\\
…\\
x_m^Tw\\
\end{bmatrix}=
\begin{bmatrix}
z_w(x_1)\\
z_w(x_2)\\
…\\
z_w(x_m)\\
\end{bmatrix} \tag{7}
$$
$$
Xw-\overrightarrow{y}=
\begin{bmatrix}
x_1^Tw\\
x_2^Tw\\
…\\
x_m^Tw\\
\end{bmatrix}-
\begin{bmatrix}
y_1\\
y_2\\
…\\
y_m\\
\end{bmatrix}=
\begin{bmatrix}
z_w(x_1)-y_1\\
z_w(x_2)-y_2\\
…\\
z_w(x_m)-y_m
\end{bmatrix} \tag{8}
$$
由矩阵内积可得
$$
\because z^Tz=\sum_i^nz_i^2 \tag{9}
$$
$$
\therefore \frac{1}{2}(Xw-\overrightarrow{y})^T(Xw-\overrightarrow{y})= \frac{1}{2}\sum_{i=1}^n(z_w(x_i)-y_i)^2=f(w) \tag{10}
$$
则梯度为
$$
\begin{equation}
\begin{split}
&\nabla_wf(w)=\nabla_w\frac{1}{2}(Xw-\overrightarrow{y})^T(Xw-\overrightarrow{y})\\
&=\frac{1}{2}\nabla_w(w^TX^TXw-w^TX^T\overrightarrow{y}-\overrightarrow{y}^TXw+\overrightarrow{y}^T\overrightarrow{y})\\
&=\frac{1}{2}\nabla_wtr(w^TX^TXw-w^TX^T\overrightarrow{y}-\overrightarrow{y}^TXw+\overrightarrow{y}^T\overrightarrow{y}) \\
&=\frac{1}{2}\nabla_w(trw^TX^TXw-2tr\overrightarrow{y}^TXw) \\
&=\frac{1}{2}(X^TXw+X^TXw-2X^T\overrightarrow{y})\\
&=X^TXw-X^T\overrightarrow{y}=X^T(Xw-\overrightarrow{y})\\\\
&=>J(w)=-f(w)=X^T(\overrightarrow{y}-Xw)
\end{split}
\end{equation} \tag{11}
$$
说明:
第二步:类似于括号展开
第三步:实数的迹等于它本身
第四步:因为 $\overrightarrow{y}^T\overrightarrow{y}$ 不含w,因此它对w求导为0.并且利用了公式 $trA=trA^T$ 进行简化。
第五步:利用公式 $\nabla_{A^T}trABA^TC=B^TA^TC^T+BA^TC$ ,令 $A^T=w,B=B^T=X^TX,C=I$ ,利用公式转化即可得到。
最后再回到《机器学习实战》中,P78,代码清单5-1②的部分。
dataMatrix=X;
weights=w;
labelMat=y;
把等号右边的用左边的变量代入,不过很遗憾,还是有些区别的,在《机器学习实战》一书中,还有sigmoid这一函数,查阅了一些资料,发现其实还是有些区别的,将于下一篇博文中阐明。
参考
吴恩达《机器学习》notes1
周志华《机器学习》chapter3 线性模型