Posted on | In ,


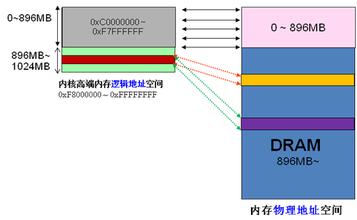
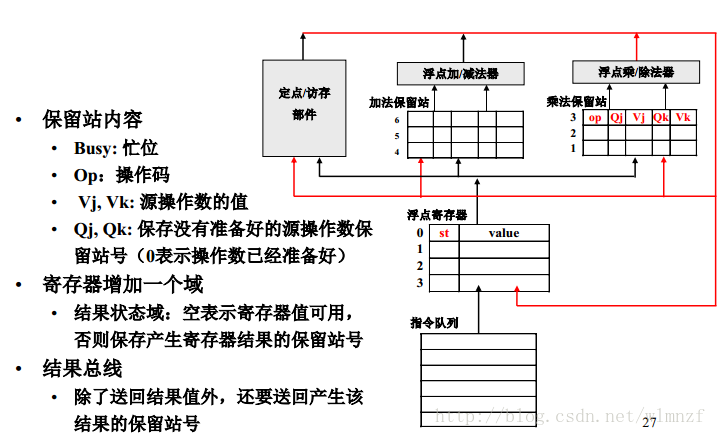
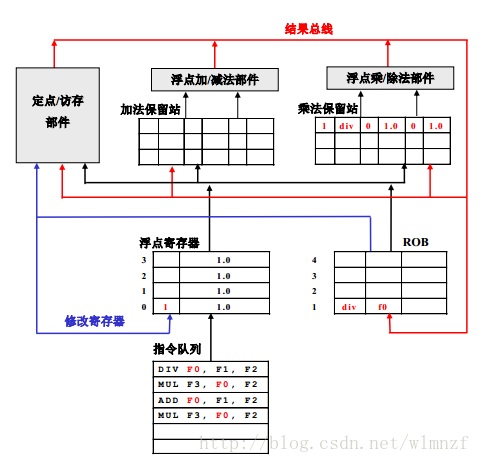
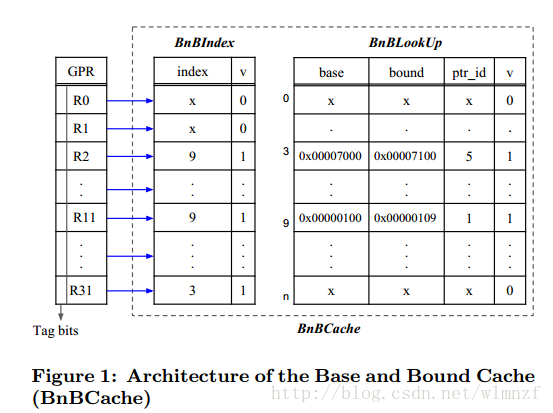
模型检验-计算树逻辑（CTL）小例
==================

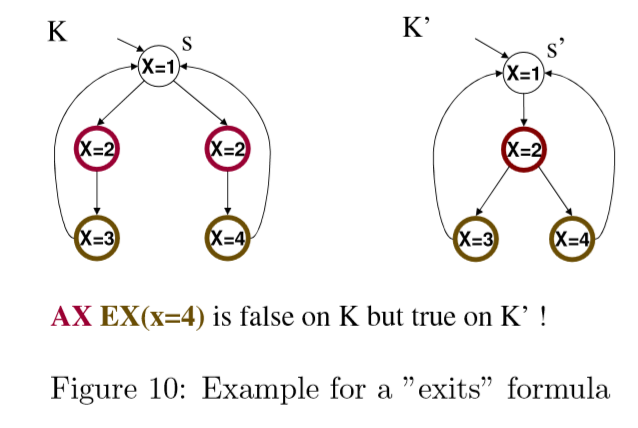
        AX是相对于初始节点（x=1）开始的树而言的，由于AX表示对于任何从初始节点(x=1)开始的路径中的下一个节点，因此EX则是相对于初始节点的子节点（x=2）开始的子树而言的。EX(x=4)表示存在从节点(x=2)开始的路径，使得子树的初始节点(x=2)的下一个节点是节点(x=4)。
        在Kripke结构K中，对于(x=1) => (x=2) => (x=3) => (x=1)的路径而言(x=2)的下一个节点是(x=3)并不满足EX(x=4)，并不是对任何从初始节点(x=1)出发的路径都满足式子中的AX。因此K不满足式子AX EX(x=4)。相反K’中对于节点(x=2)而言，存在路径 (x=2) => (x=4) => (x=1) => (x=2)满足EX(x=4)，同时它也满足AX。因此K’满足。

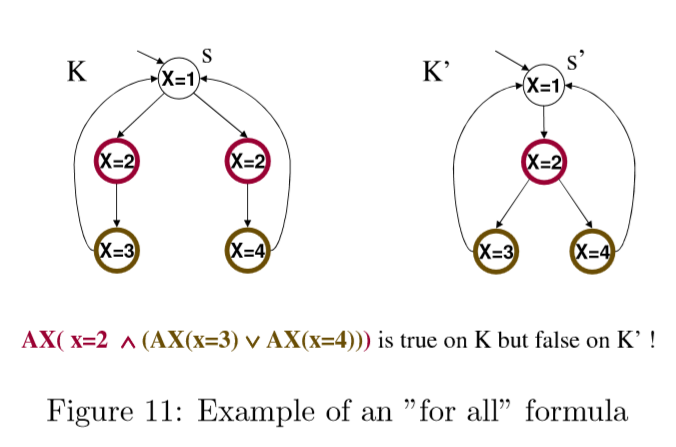
        AX(x=3) V AX(x=4)要求在K’中，从(x=2)出发的任何路径，下一个节点都是(x=3)或者都是(x=4)。但是K’中(x=2)节点的下一个节点或是(x=3)或是(x=4),并不满足条件。

Posted on | In


SPEC2006常见用法和问题
==================

安装步骤

1
2
3
4
# Ubuntu16.04
# 注意安装gFortran
. ./install.sh
. ./shrc

        一般情况下经过以上步骤即可安装完毕，进行使用,注意需要执行shrc设置完环境变量以后才可正常执行后续的各种操作。

        此外SPEC官方并不建议使用root权限，因为所有的测试集并不需要修改系统文件。

常用命令

runspec int –noreportable –n=1 –size=test

  • 正式运行SPEC2006之前需要跑一下test尺寸，test尺寸比较小，因此跑起来耗时教短，可用于确保所有测试集都可正常编译运行。
  • int：表明这是整数测试集，这个参数也可用fp，all代替，分表表示只使用浮点测试集和所有测试集。
  • –noreportable 不生成报告 –reportable生成报告，若开启将会生成诸如html，pdf等格式的报告。
  • –n=1:表示只跑一轮，每个测试集只会跑一遍。若要生成报告，则至少跑3轮
  • –size=test：表示这次只跑少量集合，用于测试所有集合是否都已经编译执行正确

runspec int –reportable –size=ref -I

  • -I 表示跑benchmark的适合忽略错误，如果中途出错也不会停下来。
  • 如果没有指定rate和copies则为测试speed，speed只能测试单核性能。
  • 若想测试多核性能，则可通过 –rate=128进行指定，这里讲使用128个线程。
  • rate和speed指标的区别请看
    Q15. What is the difference between a “rate” and a “speed” metric?

如何检测自己的电脑是多少核心的呢？

  • 逻辑CPU核心数(包括超线程技术): 

    1
    cat /proc/cpuinfo |grep "processor"|sort -u|wc -l

  • 物理CPU个数:

    1
    grep "physical id" /proc/cpuinfo|sort -u|wc -l
或者
1
grep "physical id" /proc/cpuinfo|sort -u

  • 每个物理CPU上的真实内核个数：

    1
    grep "cpu cores" /proc/cpuinfo|uniq

  • 每个物理CPU上逻辑内核个数：

    1
    grep "siblings" /proc/cpuinfo|uniq

  • 若每个核心上的逻辑内核比真实内核多，则说明开启了超线程技术

  • 来源Linux读取CPU信息

runspec 481 –noreportable –n=1

  • 有时候为了修复编译错误，可以让他单独跑481这一项

runspec -c xxx.cfg

  • -c用于指定配置文件，如果没有指定，则默认使用根目录的config文件夹下的default.cfg作为配置文件

常见错误

gcc5.x如何跑SPEC2006

  • 在无法通过的测试集的gcc编译选项上加 –std=gnu89

缺少库文件

  • 在gcc的编译选项上加 -include /usr/include/memory.h include 后面的路径需要换成自己的，这里只是举个例子

447.dealII 遇到 error: ‘ptrdiff_t’ does not name a type

  • linux下需要引入 头文件，使用上述方法在config文件中找到447.dealII的配置在CXXPORTABILITY后面加上 -include cstddef -include cstdlib -include cstring
  • 进入的头文件若是系统库，则不需要具体路径

spec2006 fp test failed with 416.gamess and 481.wrf

  • 416 miscompare 问题是gcc旧版本的bug，当开启O2优化的适合会出错
  • 升级新版本gcc或者用-O0进行编译或者换一个编译器
  • 483 end of file 问题，我是通过把配置文件中的
    1
    2
    3
    4
    5
    6

    #### 如果不幸需要自己编译工具链，可能会遇到更多奇怪的问题

    > Specmd5sum multiple definition of `getline'

    - Specmd5sum文件夹中的库文件跟系统库文件的函数冲突了，打开md5sum.c，注释掉```#include "getline.h"

在perl中make时遇到 MAKE: *** NO RULE TO MAKE TARGET ‘<COMMAND-LINE>‘

  • 这是因为gcc在高版本中改变了输出，以至于这里没有及时过滤掉，其实只要将makefile（注意不是Makefile）中<command-line>
    的那一行全删掉即可。
  • 这里有个问题是，buildtools每次编译都会将之前生成的东西清空，然后重新生成makefile文件，因此手工删除makefile中的会失败。

  • 于是自己随便在网上找了一段代码用于删除makefile文件中的’<command-line>‘

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    #include <stdio.h>
    #include <stdlib.h>
    #include <string.h>
     
    void Delete(char* filepath, char str[])
    {
    	char buf[4096];    //每读取一行，都将内容放到该数组中
    	FILE* fp = fopen(filepath, "r");     //filepath里是原内容 
     
    	FILE* fpt = fopen("temp", "w");    //将filepath文件第n行内容删除后存入temp.txt中 
    	
    	while(!feof(fp)) 
    	{  
    	   fgets(buf,sizeof(buf), fp);  
    		if (!strstr(buf,str)) 
    		{      
    		  fprintf(fpt, "%s", buf); 
                      printf("%s\n",buf);
    		}
    	} 
    	fclose(fp);
    	fclose(fpt);
     
    	fpt = fopen("temp", "r");
        fp = fopen(filepath, "w");
        fgets(buf, sizeof(buf), fpt);	
        while(!feof(fpt))
    	{
    	   fprintf(fp, "%s", buf);
           fgets(buf, sizeof(buf), fpt);
    	}
     
    	fclose(fp);
    	fclose(fpt);
     
    }
     
     
     
    void main()
    { 
    	Delete("x2p/makefile", "command");  
        Delete("makefile", "command"); 
    }

  • 将上述代码另存为delete.c,置于工具链中的perl-5.8.7根目录下

  • 并修改buildtools中的shell脚本,如下打加号的部分
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
      DYLD_LIBRARY_PATH=`pwd`
      export LD_LIBRARY_PATH DYLD_LIBRARY_PATH
      ./Configure   -dOes -Ud_flock $PERLFLAGS -Ddosuid=undef -Dprefix=$INSTALLDIR -Dd_bincompat3=undef -A ldflags=-L${INSTALLDIR}/lib -A ccflags=-I${INSTALLDIR}/include -Ui_db -Ui_gdbm -Ui_ndbm -Ui_dbm -Uuse5005threads ; testordie "error configuring perl"

    +  gcc -o del delete.c
    +  ./del
    +  cd x2p
    +    $MYMAKE
    +  cd ../
    +  ./del

      $MYMAKE; testordie "error building perl"
      ./perl installperl; testordie "error installing perl"

Posted on | In


形式化验证调研报告
==================

王立敏

中国科学院信息工程研究所 第五实验室 北京 中国100093

摘要2018年初，Spectre和Meltdown漏洞的发现，使得芯片安全备受重视。然而传统的基于仿真的芯片验证方法由于测试样例覆盖不完全，验证过程耗时巨大，逐渐适应不了日益复杂的芯片了。形式化方法作为一种静态验证方法，正好可以解决这些问题。本文主要梳理了当前形式化方法检测的常见方法，并且列出他们的优缺点，以及前人对这些缺点的改良方法。

关键词
芯片安全，形式化验证，二元决策图，时序逻辑，Petri网，定理证明，等效性检验，模型检验

Formal Verification Investigation Report

Wang Liming1


Institute of Information Engineering, Chinese Academy of Sciences, Beijing 100093, China

Abstract At the beginning of 2018, the discovery of Spectre and Meltdown attacks made chip security receive much more concerns. However, due to the serious drawbacks in the simulation-based methods in tradition such as the test cases did not cover all of the inputs and the time consuming of the simulation, this method became inappropriate to validate the chips that became more and more complicated. Formal Methods is a static verification method, which would solve these problems that the simulation-based methods bright. This report would list their advantages and disadvantages, as well as the previous methods that attempt to solve these problems.

Key words Chip security, Formal verification, Binary Decision Diagrams,Temporal logic, Petri net, Theorem Proving, Equivalence Checking, Model checking

1 引言

        近些年来，芯片的性能和规模不断提升，集成电路的设计也越来越复杂，使得引入错误和问题的可能性日益增加。但是传统的基于仿真的集成电路验证方法的覆盖率难以达到100%。而形式化方法作为一种静态测试的方法，通过数学的推理证明，理论上可以实现绝对安全，找出难以发现的错误，因此广受研究人员的关注。

基于仿真的集成电路验证

        目前应用最广泛的依然是基于仿真的验证方法。这种验证方法通常需要一个测试基准，通常同时对待验证的电路和测试基准施加相同的激励，然后通过对比他们的输出来判断电路是否正确。这些输入向量可以事先生成，然后在测试期间从数据库读入，也可以边测试边生成。

        基于仿真的验证只能证明电路在指定的输入向量下输出正确，若要证明电路的正确性，输入向量必须覆盖电路的所有输入组合。但是现在集成电路十分复杂，要实现这一点是十分困难的。令人遗憾的是，许多不安全的因素或者错误都是出现在测试向量难以覆盖的地方[1]。而且这种验证方式主要用于发现逻辑漏洞，而并不能检查出芯片中的安全漏洞。

基于形式化方法的验证

        基于形式化方法的验证是通过数理逻辑推理的一种方法。一般分为形式等效性检验（Equivalence
Checking），定理证明（Theorem Proving）以及模型检查（Model
Checking），如图1所示。

图1 形式化方法的分类

图1 形式化方法的分类

        形式等效性检验一般用于检测两个电路设计逻辑相等，电路设计一般使用硬件描述语言（Verilog或者VHDL）进行描述，然后综合成门级电路，接着再进行一系列的优化。这里的每一个步骤都会导致电路设计的改变，因此检查每一步操作前后的电路设计是否逻辑等效是有必要的。有些时候优化操作需要人为干预，因此也需要使用等效性检验来确保这些操作没有引入错误。除此之外，设计完成的芯片也需要与对应的黄金模型进行对比，以确保集成电路设计的正确性。

        定理证明方法是一种将模型抽象为逻辑公式，然后使用自动的逻辑推理技术来验证电路是否正确的技术。但是定理证明方法在使用时需要专业人士事先制定大量的定理和推理策略。因此它在自动化推理方面能力较差，不适用大规模的系统。

        模型检验是一种基于状态迁移系统的自动验证技术。它最早是由Edmund M.
Clarke和他的研究生E.A. Emerson以及A.P.Sistla提出来的[2]。使用这种方法首先需要提出一系列规格属性，这些属性表示对电路的安全需求，系统只要满足这些属性，就能确保安全。然后建立一个电路系统的模型，即可通过模型检测方法自动地检测模型是否满足这些规格属性。模型检验一般用于电路和协议的验证。

总结

        基于仿真的集成电路验证需要输入向量，而形式化验证并不需要。前者是先生成输入向量，再验证输出向量，而后者的考虑方向则相反，要先指明什么样的输出是符合要求的，再利用形式化方法去证明它。由于基于仿真的集成电路验证存在覆盖率不能达到100%，以及仿真时间过长等问题，而形式化证明则正好能解决这些问题。因此形式化验证开始被研究人员广泛关注。

模型的建立

        要使用形式化方法，需要先为电路建立模型，这些模型通常用一些图的数据结构或者公式来表示。形式化模型建立完成后，即可使用形式化算法对其进行检验。

二元决策图
2.1.1 二元决策图概述

        二元决策图（Binary Decision Diagrams，BDD）可以很好地表示一个布尔函数。所谓布尔函数，即定义域和值域都是布尔值的函数，布尔函数在电路设计和密码学方面有广泛的应用。由于电路的输入和输出都是二进制值，这意味着电路可以表示成一个布尔函数，因此使用BDD结构来表示电路是十分合适的。

2.1.2一个例子

表1 f(x1,x2,x3)的真值表

x1 x2 x3 f(x1,x2,x3)
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 1
1 0 1 0
1 1 0 0
1 1 1 1

        假设有一个电路，电路的功能如公式(1)所示。
$$
\begin{equation}
f(x1,x2,x3)=x1x2+x1\overline{x2}\overline{x3} \tag{1}
\end{equation}
$$

        其真值表如表1所示。于是可得出该电路的BDD图，如图2，x1,x2,x3为变量，实线表示变量赋值为1，虚线表示变量赋值为0。

        由表1真值表可得，当x1,x2,x3分别赋值为0时，f(x1,x2,x3)的值也为0。则如图2在BDD图中沿着x1,x2,x3,0之间的虚线最终也会到达0的地方。如图中所示这样变量有序的BDD图也可以称作有序二元决策图（Ordered Binary Decision Diagrams ，OBDD）图。

        可以发现，当x1赋值为0,x2也赋值为0时，无论x3赋何值，最终结果也是0，因此可以将BDD再做精简。如图3中简化后的BDD所示，可以将这条路径中的x3节点删除，直接将x2用虚线连接至0处，这个过程可称为BDD的简化，而最终的简化结果则称为简化的有序二元决策图（Reduced
Ordered Binary Decision Diagrams，ROBDD）。

图2 f(x1,x2,x3)的BDD图

图2 f(x1,x2,x3)的BDD图

图3 f(x1,x2,x3)的简化BDD图

图3 f(x1,x2,x3)的简化BDD图

2.1.3基于二元决策图的电路表示

        对于组合逻辑电路而言，可以直接使用上述方法生成BDD结构。但是对于时序逻辑电路而言，则需要根据其特点生成有限自动机（Finite State Machine，FSM），再使用BDD来表示FSM的状态变迁过程，在形式等效验证和符号模型检验中常采用这一方法来表示电路。

        BDD本身不能减少状态空间，随着变量数的增加，状态空间数依然呈指数级上涨，但是它也有许多优点，比如表达形式简洁，并且配合图算法可实现快速的操作，用于表示电路十分合适。

时序逻辑

        时序逻辑是逻辑领域中一个重要的组成部分，它在形式化验证中有十分重要的应用

表2 时序逻辑的操作

符号 操作 解释
θUψ Until 若θUψ在路径上为真，则θ一直保持真直到ψ为真
θRψ Release 若ψ为真，直到θ为真（或者θ永远不为真）则θRψ在路径上为真，
Xθ Next 若Xθ在路径上为真，则下一个时刻θ为真
Fθ Future 若Fθ在路径上为真，则θ最终一定为真
Gθ Globally 若Gθ在路径上为真，则任何时刻，θ都为真
Aθ All 表示对于任意路径
Eθ Exists 表示存在这样的路径

        可以使用如表2所示的符号来描述硬件系统的行为，例如我们要表示“信号A一直不变，直到上升沿才翻转”这一操作，则我们令p为“信号A不变”，q为“时钟到达上升沿”，则该操作可表示为当满足pUq使信号A翻转。

        比较常用的时序逻辑是线性时序逻辑（Linear temporal logic，LTL）以及计算树逻辑（Computation tree logic，CTL）。线性时序逻辑是个线性结构，每一个时刻都只对应一个后继，计算树逻辑则是一个树状的分支结构。LTL可用于重点对象的分析，并且它可以使用公平的概念，但是对于一些可返回到初始状态的复杂系统，LTL则无法表示。CTL则相反，它无法使用公平的概念，但是却可以表达一些较为复杂的系统[3]。LTL和CTL各有自己的优势，E. A. Emerson 和 Joseph Y. Halpern 在 1986年提出了CTL*，统一了LTL和CTL。在传统的模型检验中，通常采用时序逻辑来描述电路。

Petri网

        Petri网是一种重要的数学工具，Petri网对系统的并发性，异步性和不确定性具有很强的描述能力，一般主要是使用Petri网的可达图[4]。

Petri网通常为四元组N= \<P,T,F,M0>

P：库所（Place）的有限集

T：迁移（Transition）的有限集

F：F ⊆ (P x T) ∪ (T x P)，表示边的集合。∪前后分别表示输入函数集以及输出函数集。

M0：P->N，表示初始状态集

库所（Place）表示系统的状态。一般用

表示。

迁移（Transition）则表示资源的消耗使用，一般用 表示。

        连接库所与变迁的有向弧表示输入输出函数。用令牌Token表示库所中的资源数量，一般用●表示。

        资源会沿着有向弧流动，当资源足够时，便会触发某些操作的执行来使用和消耗资源。即令牌会不断沿着迁移流动，令牌在迁移之前积聚叫做迁移的使能（enabled），令牌积累到足够数量之后便能通过迁移，这一过程也叫迁移的激发(fire)。

        图4表示一个互斥系统的Petri网，双方发出进入临界区的请求，当其中一方进入临界区时，另一方只能等待。图中的小黑点表示Token，最中间的库所t表示哪一方可优先访问临界区，当Idle中的Token传递到Wait时，t中个Token也会流到可优先进入临界区的那一方，于是便可以激发迁移Access，当经过Free之后，Token又将回到Idle和t中。

图4 互斥模型的Petri网

图4 互斥模型的Petri网

1.形式化方法

形式等效验证（Equivalence Checking）

        假设我们有Spec1和Spec2两个模型。若需要验证综合优化前后两个模型是否逻辑相等，则Spec1和Spec2可分别表示综合优化前后的设计。若需要验证设计的正确性，Spec1通常为黄金模型，Spec2则为我们的设计。Spec1和Spec2通常使用相同的数据结构，例如BDD，再根据具体的需求使用诸如布尔SAT求解程序（求解可满足性问题）之类的算法来进行等效性检验。

        虽然等效检验的检测效果不错，在工业上也得到了应用，但是在使用过程中依然需要高层次的专业人员去制定等效检验框架[5]。而且在复杂的电路中，等效性检验也存在状态空间数呈指数级增长的问题。虽然学术界提出了各种优化的方法，比如将复杂的等效检验切割成小的可比较集合进行处理[6]，或者利用算法优化减少空间消耗[7]，但是状态空间爆炸问题依然没有很好地解决。

定理证明(Theorem Proving)

        定理证明方法十分严格，跟数理逻辑结合十分紧密。一般使用高阶逻辑（Higher-Order
Logic，HOL） 系统来进行证明。

        要验证一个大的系统，通常采用目标制导的方式。将系统用HOL表示出来之后，再分为若干个子命题分别证明。定理证明方法对硬件模块的验证一般会用到抽象技术和层次化验证技术

        在证明之前需要对系统进行建模，Mike Gordon在论文[8]中提出可以直接利用HOL来为硬件建模。一个器件模块只有输入输出，这些输入输出可以用HOL中的谓词和函数表示，而模块之间的连接可用合取表示。

        抽象技术主要用于将系统的详细信息掩盖掉，只考虑需要关注的性质，这样可以方便算法的处理。根据关注对象的不同，可以分为不同的抽象。例如结构抽象掩盖了内部结构信息而只描述了设备的规范，而行为抽象则只对模块的部分行为进行定义，数据抽象则是通过一个映射，将现实中的数据抽象为一个较小的抽象数据集，比如布尔真值。

        层次化验证技术是将大的模型划分为小的模型，构建成一个树状结构，每一个子节点都是父节点的细化。下一层的正确性可以证明上一层的正确性，因此自下而上地证明可以确保根节点的模型的正确性。

        定理证明方法在工业上也有一定的使用，但是定理证明方法需要对系统用严格语义的数学符号进行描述和推理，因此对用户而言十分复杂。而且并没有办法确保事先人为制定的规则和定理的正确性，因此最终的正确性也值得怀疑，即前提若有错误，则最终的验证结果就不一定正确。

模型检验(Model Checking)

        模型检验是目前最为流行的形式化检测方法。但是它依然存在状态空间爆炸的问题，模型检测方法的发展几乎都是为了解决状态空间爆炸问题以及不同系统的适用性问题展开的。

        状态空间爆炸问题一直制约着模型检验方法的发展，为此科研人员一直寻找合适的方法来解决这一问题，例如符号模型检验，偏序规约技术，以及近些年来十分热门的SAT技术。

3.2.1符号模型检验

        符号模型检验的提出是解决状态空间爆炸问题的一个里程碑，它采用OBDD来描述电路。这使得模型检验可检查的系统规模大大增加，可以超过1020个状态。

        McMillan最先将OBDD引入模型检验技术[9]，提出了符号模型检验，最初时符号模型检验只是基于CTL公式的。该方法将CTL公式转化成OBDD图，并在OBDD上搜索状态空间。之后Clarke等人又提出了基于LTL的符号模型[10]。

        符号模型检验中，存在许多优化方法，最常见的两种方法是偏序规约技术[11]和抽象模型[12]。

        由于系统中可能存在两个并行的模块，而这些并行模块的运行组合有许多种，其中的一部分运行组合实际上是重复的。因此若能将并行的模块的运行次序固定下来，在验证过程中就可以减少许多重复的路径。

        抽象技术多用于需要数据处理的系统，符号模型检验的数据处理能力较弱，若是需要表达复杂的数据结构，则验证的复杂性会十分的高。因此可以将精确的数据值和抽象的数据集合做个映射，产生一个较小的抽象数据集，以此来简化符号模型检验的状态空间。

3.2.1 SAT技术

        基于BDD的符号模型检验虽然使得可检验的系统规模增加了许多，但是状态空间爆炸问题并没有彻底解决，在BDD中，状态空间依然是指数级增长的。BDD可通过简化生成ROBDD来减少状态空间，但是可优化的余地依然比较少。随着SAT技术的发展，它也被引入到模型检验领域[13]。

        SAT是NP完全的方法，因此它也是指数爆炸型的，为此Clarke等人提出了限界模型检验[14]。模型检验是通过对整个系统建模，并证明我们的模型是否满足我们定义的属性规格。而限界模型检验，则通过广度搜索的方法，从长度为1的路径开始搜索，搜索的路径长度逐渐递增，若能在长度为K的路径中搜索到不符合属性规格的路径，则停止搜索并报告这一反例。

        虽然限界模型检验搜索到反例后即可停止这一机制使得其遍历的状态大大减少，但是它只检查了整个状态空间的一个子集，只能证明在限界中的那部分状态符合属性规格，而无法证明整个状态空间符合属性规格。

        为了解决这一完整性问题，目前学术界较为流行的做法是逼近所求的解，即迭代地计算可达状态的不动点，来验证这整个模型是否最终满足规约。

        Yakir Vizel等人于2015年整理了各种适用于SAT的优秀的算法，这些算法包括冲突驱动从句学习（Conflict-Driven
Clause Learning），随机局部搜索（Stochastic Local Search）[15]。

        SAT技术在经过EDA社区与科研人员的相互促进之下，在过去十年中取得了很大的进步。虽然SAT在工业界也得到了应用，但是它依然无法很好地解决模型检验的状态空间爆炸问题和限界模型检验的完整性问题，此外并行SAT技术也是一个十分有前景的方向。

        而为了解决不同系统的适应性问题，如第2部分所述，研究人员提出了许多不同的建模方式。传统的模型检验方法一般采用时序逻辑来描述电路。

4 讨论

        传统的基于仿真的验证方式虽然存在有覆盖不完全，耗时间等问题。而形式化验证则正好可以解决这些问题，然而这并不意味着形式化方法可以完全替代传统的仿真验证。形式化方法依然存在许多的局限性，目前最好的办法是将传统的仿真验证与形式化验证结合起来。

        虽然在工业界和学术界的共同促进之下，形式化验证技术有了长足的进步。但依然存在不少进步的空间。模型验证是目前自动化水平最优的，很少需要手动干预，但是状态空间爆炸的问题依然令人十分困扰。为了提高形式化验证的速度,研究人员依然在尝试攻克检测技术的并行化的问题，这也是目前较为火的一个方向。此外为了能够使用到工业界，形式化验证必然还是需要提高检测技术的自动化水平，例如门级信息流的方法[16]利用关键信息只能从低安全级流向高安全级这一特性，简化了形式化方法建模的流程，使其可以自动生成模型。此外，纵观整个形式化验证方法的发展历程，可以发现许多形式化验证的突破，都是因为将一些已经存在的理论成果移植应用到工程中去，因此我们也可以从这一方面去考虑如何改进形式化验证的方法。

        形式化方法是个十分有前景而又十分重要的研究方向，不仅可以用于检测出难以发现的逻辑错误，也可以检查电路中隐藏的硬件木马，甚至发现较为隐秘安全漏洞。因此上述的一些形式化方法的局限依然值得我们在日后重点研究。

参考文献

[1] LAM W K. Hardware Design Verification: Simulation and Formal Method-Based
Approaches (Prentice Hall Modern Semiconductor Design Series)[M]. Upper Saddle
River, NJ, USA: Prentice Hall PTR, 2005.

[2] CLARKE E M, EMERSON E A. Design and synthesis of synchronization skeletons
using branching time temporal logic[J]. : 20.

[3] 张瑞雪, 郝春梅, 王旭. 计算机形式验证方法研究综述[J]. 中国电子商务, 2011(5):
69–69.

[4] 蒋屹新, 林闯, 邢栩嘉. 基于线性时态逻辑的Petri网模型检测[J]. 系统仿真学报,
2003, 15(z1): 6–10.

[5] KREIKER J, TARLECKI A, VARDI M Y等. Modeling, Analysis, and Verification -
The Formal Methods Manifesto 2010 (Dagstuhl Perspectives Workshop 10482)[J].
HERBSTRITT M. 2011.

[6] KUEHLMANN A, KROHM F. Equivalence Checking Using Cuts and Heaps[J]. : 6.

[7] PARUTHI V, KUEHLMANN A. Equivalence checking combining a structural
SAT-solver, BDDs, and simulation[C]//IEEE Comput. Soc, 2000: 459–464.

[8] HAN J, STONE G. The implementation and verification of a conditional sum
adder[J]. 1988.

[9] MCMILLAN K L. Symbolic checking，An approachto the state explosion
problem[J]. : 212.

[10] CLARKE E, GRUMBERG O, HAMAGUCHI K. Another look at LTL model
checking[C]//International Conference on Computer Aided Verification. Springer,
1994: 415–427.

[11] PELED D. All from one, one for all: on model checking using
representatives[G]//COURCOUBETIS C. Computer Aided Verification. Berlin,
Heidelberg: Springer Berlin Heidelberg, 1993, 697: 409–423.

[12] CLARKE E M, GRUMBERG O, LONG D E. Model checking and abstraction[J]. ACM
transactions on Programming Languages and Systems (TOPLAS), 1994, 16(5):
1512–1542.

[13] 王瑞. 基于SAT的符号化模型检验技术研究[D]. 国防科学技术大学, 2014.

[14] CLARKE E, BIERE A, RAIMI R等. Bounded Model Checking Using Satisfiability
Solving[J]. : 20.

[15] VIZEL Y, WEISSENBACHER G, MALIK S. Boolean Satisfiability Solvers and Their
Applications in Model Checking[J]. Proceedings of the IEEE, 2015, 103(11):
2021–2035.

[16] HU W, MAO B, OBERG J等. Detecting Hardware Trojans with Gate-Level
Information-Flow Tracking[J]. Computer, 2016, 49(8): 44–52.

Posted on | In


梅森旋转算法安全性分析及改进
======================

王立敏1,丁洁2

1中国科学院信息工程研究所 第五实验室 北京 中国100093

2中国科学院信息工程研究所 第五实验室 北京 中国100093

摘要
梅森旋转算法是目前最流行的伪随机数发生器算法之一。梅森旋转算法存在许多缺点，例如当生成的伪随机数数量庞大时可预测以及无法通过部分统计测试。为了更好地深入了解和分析梅森旋转算法的安全性，本文将使用NIST
800-22文档中提到的统计测试等方法来对其生成的伪随机数进行静态的质量评估，并通过伪代码对该算法进行理论安全分析。由于梅森旋转算法生成伪随机数的速度十分快，而且开发者和研究人员们已经开发了许多梅森旋转算法的改进版本，甚至密码学安全的版本，因此当需要伪随机数时，选用梅森旋转算法作为伪随机数生成器是合理的。

关键词 梅森旋转算法，MT19937标准，统计测试，安全性分析

The Analysis And Improvement Of Mersenne Twister

Wang Limin1, Ding Jie2

1Institute of Information Engineering, Chinese Academy of Sciences, Beijing 100093, China


2Institute of Information Engineering, Chinese Academy of Sciences, Beijing 100093, China

Abstract Mersenne Twister is one of the most useful pseudo random number generator algorithms. There are many shortcomings in Mersenne Twister. For example, it would be predictable and could not pass some of statistical tests when the algorithm generates plenty of pseudo random number generator algorithms. To analyze the security of algorithm, the statistical tests mentioned in NIST 800-22 would be used to evaluate the quality of Mersenne Twister and the pseudocode would be used to analyze the security of the algorithm. Mersenne Twister is very fast, and the developers and researchers have developed the improved versions of this algorithm, even the cryptographically secure version. For these reasons, choosing Mersenne Twister as the alternative pseudo random number generator is reasonable.

Key words Mersenne Twister, MT19937, statistical test, the analysis of security

1 前言

        随机数在许多领域中都有着大量应用，例如密码学，游戏，数学统计。随机数主要分两类，分别是确定性随机数和非确定性随机数。非确定性随机数也可称为真随机数（True Random Number Generator, TRNG），主要来源于不可预测的物理或者化学熵源，例如电路噪声。真随机数发生器产生的随机数质量十分高，是最理想的随机数来源，但是由于产生的速度太慢，无法满足目前的信息的传输速度，因此目前确定性随机数依然被广泛使用。确定性随机数发生器也称作伪随机数发生器（Pseudorandom Number Generator，PRNG）,它一般是一个随机数生成算法，由于算法是固定的，因此生成的随机数存在许多诸如可预测，质量不高的缺点。因此在使用一个伪随机数发生器之前对其进行评估是十分有必要的。

        梅森旋转是目前应用十分广泛的伪随机数生成器算法之一，已经集成在C++等编程语言的标准库中。梅森旋转生成的随机数能通过常见的静态统计测试，并且生成速度十分快，但是它依然存在许多缺点，例如当随机数数量足够时可预测。本文主要对该方法进行质量评估和安全性分析，并且提出一些改进意见。

2 梅森旋转

        MT19937以及MT19937-64标准分别实现了梅森旋转的32位以及64位算法，由于这两者只是参数不同，因此为方便起见，只实现和讨论MT19937标准。MT19937标准采用的梅森素数为219937
-1，因此它可生成的随机数范围为[0, 219937 -1]。

        梅森旋转算法实际使用的是旋转的广义反馈移位寄存器（Twisted Generalized Feedback Shift Register,GFSR）[2]，它主要分初始化，旋转生成随机数以及Xorshift后期处理三个步骤。由于MT19937的梅森算法中生成的随机数为32位，因此算法需要624个32位长的状态。在初始化阶段，算法的工作是将我们获得的随机种子经处理填充到所有的624个状态中

算法1：初始化
输入: 一个随机种子seed 
1
2
3
4
5
6
mt[0] = seed 
a=1812433253  
FOR i FROM 1 TO 623 
  { 
     mt[i] = f * (mt[i-1] XOR (mt[i-1] >> 30)) + i    
  }

        MT19937规定了算法1中的f值为1812433253 ，算法将输入的随机种子赋值给第0个状态，剩余的623个状态则用前一状态值的一系列操作进行赋值更新。当执行完这一算法后，全部的624个状态已经填充完毕，之后梅森算法便可以不断地生成伪随机数。

算法2：旋转生成随机数 
1
2
3
4
5
6
7
8
9
10
11
12
13
lower_mask = (1 << 31) - 1, 
upper_mask = (1 << 31)
a = 0x9908B0DF
FOR i FROM 0 TO 623
  {
    x = (mt[i] AND upper_mask) +(mt[(i+1) MOD 32] AND lower_mask)
    xA = x >> 1
    IF (x MOD 2) != 0
    {
      xA = xA XOR a
    }
    mt[i] = mt[(i + 397) MOD 624] XOR xA
 }

        MT19937标准中定义a的值为0x9908B0DF，如算2所示，这部分是进行旋转操作。每生成624个伪随机数后，将执行一次算法2，重新更新624个状态，为生成下一批624个伪随机数做准备。

算法3:Xorshift后期处理
输出：生成的伪随机数y 
1
2
3
4
5
6
7
b = 0x9d2c5680 
c = 0xefc60000 
y = mt[i] 
y = y XOR (y >> 11) 
y = y XOR ((y << 7) AND b) 
y = y XOR ((y << 15) AND c) 
y = y XOR (y >> 18)

每个状态都需要经过Xorshift操作[3]以后才能成为最终输出的伪随机数，由于其中几乎都是移位，因此对CPU来说是十分快的。

3 伪随机数发生器的评估

正如前言部分所述，伪随机数发生器的评估是十分有必要的。伪随机数的质量和安全性一般有如下4个评判标准:

  1. 随机数应该有很好的统计属性。例如各态遍历性

  2. 不能根据随机数的子序列合理推出其之前或者之后的随机数序列。并且子序列不能提高推出其之前和之后的伪随机序列的可能性。

  3. 不能根据内部状态合理推出其之前的内部状态。同样的也不能通过内部状态提高推出其之前的内部状态的可能性。

  4. 不能根据内部状态合理推出其之后的内部状态。也不能通过内部状态提高推出其之后的内部状态。

梅森旋转伪随机数的质量评估

4.1 NIST 800-22测试

图1 NIST 800-22随机数测试

图1 NIST 800-22随机数测试

        NIST 800-22文档中提到了许多静态测试[4]，并且提供了测试程序NIST STS-2.1.2。David Johnston认为STS程序存在许多问题，例如经常奔溃，并且给出错误的测试结果，因此他修正了这些错误，并且给出了修正后的程序[5]。本测试采用了该自动化测试程序，在Summary一栏中左侧为测试名称，右侧为测试的统计参数P值，如图可见该梅森旋转算法可以通过文档中提到的所有静态测试。

4.2 PractRand测试

图2 PractRand随机数测试

图2 PractRand随机数测试

        PractRand也是目前常采用的测试程序。由图2所示，我们可以看到当随机数输出大小为128G时可以满足常见的静态统计测试，但是当输出随机数的数量达到256G时，BRANK测试无法通过。

4.3 安全性分析

        第三部分的算法3将状态进行移位和亦或，最终输出为伪随机数，但是这一过程是可逆的。逆过程的具体证明和分析方法可参看oupo和plusletool的博客[6,7]。

算法4: 算法3的逆过程
输出：梅森旋转的中间状态value 
1
2
3
4
5
6
7
8
9
10
11
value = y 
value = value XOR (value >> 18)
value = value XOR (value << 15) AND 0xefc60000
value = value 
       XOR ((value << 7) & 0x9d2c5680) 
       XOR ((value << 14) & 0x94284000) 
       XOR ((value << 21) & 0x14200000) 
       XOR ((value << 28) & 0x10000000) 
value =value 
       XOR (value >> 11) 
       XOR (value >> 22)

        算法4描述了如何由伪随机数逆向恢复到梅森旋转算法的状态，因此若我们有624个梅森旋转算法生成的伪随机数，则我们可以由算法4恢复得到624个中间状态。再通过算法2和算法3即可得到接下来的伪随机数了。

        但是由算法2可知，在进行旋转的时候，需要用到第i个状态，第i+1个状态以及第i+397个状态。因此如果敌手所得到的伪随机数量或者状态不足，则不能恢复所有的624个状态，便也不能继续预测接下来的伪随机数。而且算法2中的旋转操作会直接覆盖之前的内部状态，而且算法中跟mask进行与操作以及右移操作使得它无法再逆向推导出之前的状态，因此所幸的是即使敌手获取到足够量的伪随机数，也无法推出之前的伪随机数。

        梅森旋转算法可以满足常见应用的随机数需求，但是对于加密过程中所需的伪随机数，还是需要使用密码学安全的伪随机数（Cryptographically
Secure Pseudo-Random Number
Generator，CSPRNG），例如改进版的梅森旋转算法CryptMT。

5 梅森旋转的改进方案

5.1 Hash输出

        由于梅森旋转算法可逆，我们可以通过泄露的伪随机数逆向推算出其内部状态，因此若将最终输出再进行Hash处理，如图3所示，即可使其生成的伪随机数不可逆，这样便可一定程度上提高梅森旋转算法的安全性。

        Hash算法不可逆，并且可以被用来生成伪随机数[8]，生成的随机数也具有很好的安全性。此外，SHA-3之所以拥有安全，不可逆等良好的特性，是因为采用了海绵结构，而且目前已经存在基于海绵结构的伪随机数生成器了[9,10]。综上所述，Hash算法可以用于生成质量较高的伪随机数，而且不可逆，若想要更灵活方便地移植使用，则也可以直接使用海绵结构。因此改进方案中采用Hash对梅森算法的输出做最后的处理使其不可逆是合理的。

图3 经过Hash的梅森算法

图3 经过Hash的梅森算法

5.2 间隔输出

        由算法2可知，当梅森算法更新当前第i个状态时必须要用到第i+1个状态以及第i+397个状态。因此如图4所示假设将这些状态每隔一个进行处理输出为伪随机数，则即使敌手获取到大量的间隔伪随机数，并且将他们逆向恢复为算法的内部状态，也无法得到完整的624个状态。若没有完整的624个状态，则也无法继续预测生成接下去的伪随机数。

图4 间隔输出的梅森算法

图4 间隔输出的梅森算法

6 结论

        根据第3部分所描述的4个评估标准可知梅森旋转算法并不完美。它依然无法通过其中的小部分统计测试，例如当生成的伪随机数达到256G时，无法通过BRANK测试。当敌手可以获得超过624个伪随机数时，可以通过逆向推导出其内部状态来预测其接下来生成的伪随机数。不过所幸的是由于其更新内部状态时的操作不可逆，使得它无法推导出已经生成过的伪随机数。对于第四个评估标准，事实上包括梅森旋转在内的确定性的伪随机数发生器都无法满足，因为算法固定，因此只要获取到内部状态，就一定可以推算出之后的伪随机数。

        梅森旋转算法虽然存在许多的缺点，比如当获取到的伪随机数数量足够多时是可以预测的，并且无法通过一些静态统计测试。但是由于它的许多操作都是基于移位的，因此速度更快一些。并且近些年来，许多开发者和研究人员都为改进梅森旋转算法做出了许多努力，诞生了许多更优秀的基于梅森旋转算法的随机数生成器，例如CryptMT，MTGP。

        因此在通用的软件上使用改进版的梅森旋转算法，以及在加密时使用密码学安全的梅森旋转算法（CryptMT）是十分合理的。

代码请看这里

参考文献

[1] 徐恒. 确定性随机数产生器安全性分析及改进[D]. 上海交通大学, 2009.

[2] MATSUMOTO M, KURITA Y. Twisted GFSR generators[J]. ACM Transactions on
Modeling and Computer Simulation, 1992, 2(3): 179–194.

[3] MARSAGLIA G, OTHERS. Xorshift rngs[J]. Journal of Statistical Software,
2003, 8(14): 1–6.

[4] NIST S. 800-22[J]. A Statistical Test Suite for Random and Pseudorandom
Number Generators for Cryptographic Applications, 2000, 120.

[5] JOHNSTON D. sp800_22_tests: A python implementation of the SP800-22 Rev 1a
PRNG test suite[M]. 2018.

[6] PLUSLETOOL. メルセンヌ・ツイスタのtemperingの逆関数に関する考察[EB/OL]. Plus
Le Blog, 1414154296. (1414154296)[2018-07-15].
http://plusletool.hatenablog.jp/entry/2014/10/24/213816.

[7] 2014-10-16[EB/OL]. oupoの日記, [2018-07-15].
http://d.hatena.ne.jp/oupo/20141016.

[8] BOLDYREVA A, KUMAR V. A New Pseudorandom Generator from Collision-Resistant
Hash Functions[G]//DUNKELMAN O. Topics in Cryptology – CT-RSA 2012. Berlin,
Heidelberg: Springer Berlin Heidelberg, 2012, 7178: 187–202.

[9] BERTONI G, DAEMEN J, PEETERS M等. Sponge-Based Pseudo-Random Number
Generators[G]//MANGARD S, STANDAERT F-X. Cryptographic Hardware and Embedded
Systems, CHES 2010. Berlin, Heidelberg: Springer Berlin Heidelberg, 2010, 6225:
33–47.

[10] BERTONI G, DAEMEN J, PEETERS M等. Duplexing the Sponge: Single-Pass
Authenticated Encryption and Other Applications[G]//MIRI A, VAUDENAY S. Selected
Areas in Cryptography

Posted on | In


基于无保护AES芯片的 CPA攻击
===========================

王立敏1,丁洁2

1中国科学院信息工程研究所 第五实验室 北京 中国 100093

2 中国科学院信息工程研究所 第五实验室 北京 中国 100093

摘要 高级加密标准（Advanced Encryption Standard，AES）是最常用的加密算法之一。为了提升实际应用中加解密操作的速度，或者在小型芯片上完成加密工作，AES通常被集成在加密芯片中。这使得其容易遭受侧信道攻击，尤其是能量分析攻击。本文中将采用相关能量分析（Correlation Power Analysis，CPA）对AES的能量迹和字节替换环节之间的关系进行统计分析来猜测其对应的密钥。其结果表明对于普通的无保护AES芯片，CPA攻击十分有效。

关键词 侧信道攻击，AES，密码芯片，相关能量分析，能量迹

The CPA Attack For Unprotected AES Chips

Wang Limin1, Ding jie2

1 Institute of Information Engineering, Chinese Academy of Sciences, Beijing
100093, China


2 Institute of Information Engineering, Chinese Academy of Sciences, Beijing
100093, China

Abstract Advanced Encryption Standard is one of the most commonly used encryption algorithms. In order to improve the speed of encrypted and decrypted operations or encrypt data on chips , the independent AES chip is used for encryption, which makes the chip vulnerable to Side-Channel Attack, especially to Power Analysis. This paper will guess the key of the AES by analyzing the correlation between power trace and SubBytes operation. This experiment shows that CPA attack can help crack secret keys more efficiently.

Key words Side-Channel Attack, AES, Cipher Chip, Correlation,Power Analysis,Power Trace

1 引言

        侧信道分析技术在硬件安全领域中应用十分广泛。其中较为常见的一种是能量分析，它主要包括三种分析方法，简单能量分析（Simple Power Analysis, SPA），差分能量分析(Differential Power Analysis,DPA)以及相关能量分析(Correlation Power Analysis, CPA)。SPA和DPA最初由Paul Kocher, Joshua Jae, 和 Benjamin Jun 在1999年提出[1]。SPA利用的是密码芯片在进行不同的指令操作时所消耗的能量也不同这一特性，例如AES芯片在执行10轮操作时，它的10个能量消耗峰值将会十分明显。而DPA则更加复杂，它将测出来的能量迹分为几类，并计算它们均值的差，若假设的密钥是正确的，则会出现一个能量波峰，否则差值会在0附近波动。DPA是十分有效的能量攻击方法，但是它依然存在诸如幽灵峰值的问题，而本试验中给出的能量迹又足够多，因此为了提高破译密钥的正确性，本文将采用CPA来对AES进行攻击。CPA由E.Brier提出，是从DPA改进而来，它采用的是汉明重量模型[2]。

2 AES介绍

        AES在安全性不低于三重数据加密算法（Triple Data Encryption Algorithm，TDEA，也叫3DES）的同时，运算速度还比它快，因此被采用来替代原先的数据加密标准（Data Encryption Standard，DES），它具有很好的抗差分密码分析和线性密码分析的能力。AES根据密钥的长度的不同有三种不同的版本分别为AES-128，AES-192以及AES-256。本文只讨论利用CPA攻击无保护的AES-128算法，如算法1所示。

算法1：无保护的AES-128算法
输入：明文X[0-15],轮密钥RoundKey[0-10] 输出：密文X[0-15] 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
for r = 0;r ≤ 8;r++ do
     X = X ⊕ RoundKey[r]; /*加轮密钥*/
     
     for i = 0; i≤15; i++ do
       Xi = SubBytes(Xi); /*字节替换*/
     end

     X = ShiftRows(X); /*行变换*/
     X = *MixColumns*(X); /*列混淆*/

end

X = X⊕*RoundKey*[9]; /*最后一轮*/

for I = 0; i≤15; i++ do
    Xi = SubBytes(Xi);
end

X = ShiftRows（X）
X = X⊕RoundKey[10] /\*获取密文\*/

        AES-128算法需要经过10轮的操作，除了最后一轮之外，前9轮都包括加轮密钥，字节替换，行变换，列混淆这四个步骤，而第十轮则少一个列混淆。这里的11个128位的轮密钥是原始的128位密钥经过密钥扩展得到的。

2.1 密钥扩展

        密钥扩展是将最初始的128位密钥扩展成11个轮密钥，方便每一轮中的操作。假设有这样一个128位的密钥，如图1所示。然后按每4字节为一列排列成图2所示的阵列。

图1 给定的 AES密钥

图1 给定的 AES密钥

图2 密钥的排布

图2 密钥的排布

        图2中每一列分配一个标记wi，第一列为w0，第二列为w1，以此类推。每一个轮密钥的第一列生成方式都较为复杂，这里以生成第5列（w4）为例。

图3 w3左移一位

图3 w3左移一位

        如图3所示，当将最初的密钥排列完毕以后，需要将最后一列进行循环左移。并且左移后的每个元素都要经过S-BOX的字节替换处理，图四表示了这一过程。关于S-BOX字节替换的详细描述可参看2.3部分。

图4 左移后经过S-BOX进行字节替换

图4 左移后经过S-BOX进行字节替换

        假设正在生成第i列密钥，这里是第5列，即为w4。由于此处是第二个轮密钥的第一列，则经过字节替换后的结果，需要与wi-4即w0以及rcon[i/4-1]即rcon[0]进行异或才能最终得出w4。其中rcon是如图6所示的10列数字。

图5 轮密钥第一列生成

图5 轮密钥第一列生成

图6 RCON数组

图6 RCON数组

        只有轮密钥的第一列需要按照上述方法生成，接下来的三列则通过图7所示的方法，通过将wi-1以及wi-4异或来求得，例如这里轮密钥第二列w5，则是通过w4和w1异或得来的。

图7 轮密钥第二列生成

图7 轮密钥第二列生成

        之后的每一个轮密钥都将按照上述方法进行计算得出，轮密钥第一列wi=SubByte（LeftShift（wi-1））⊕wi-4⊕rcon[i/4-1],而第二，三，四列的计算规则为wi=wi-1⊕wi-4。图8即为新生成的轮密钥，可以很明显看出轮密钥0就是最开始输入的密钥，通常对AES的能量分析，都只分析第一轮，这一轮的轮密钥加操作使用的是轮密钥0，即原始输入的密钥。因此在进行CPA攻击时不需要经过密钥扩展这一步。

图8 新生成的轮密钥

图8 新生成的轮密钥

2.2 加轮密钥

        AES经过密钥扩展得到轮密钥之后，将进行10轮操作，在每一轮操作中都需要加轮密钥。首先需要将明文和轮密钥按4字节为一列排成4列，分别命名为P0-P15和C0-C15,然后将明文和密文，按字节进行异或，即P0⊕C0-P15⊕C15。得到的最终结果可用于后续的字节替换。

图9 轮密钥加

图9 轮密钥加

2.3 字节替换

        字节替换一般使用的是Rijndael S-box[3],它将需要替换的字节的高四位作为横坐标，低四位作为纵坐标从S-BOX中选中对应的字节作为替代值。

        如图10，待替代字节为0x01,则横坐标为高四位0x0,纵坐标为低四位0x1，从S-BOX中找到对应坐标的值0x7c，然后将其替换，图10展示S-BOX的替换过程，其中的S-BOX只是完整表格的一部分。

图10 S-BOX替换

图10 S-BOX替换

3 CPA攻击

        CPA攻击主要采用汉明重量模型。计算汉明重量与对应能量迹之间的相关系数，若相关系数越大，则说明他们之间的相关性越强，若数据中某一猜测密钥对应的相关系数相比于其他相关系数要大的多，就可以说明这一猜测密钥是正确的。

3.1 汉明重量

        汉明重量可以表示一个二进制字符串中1的个数。已经有论文通过实验证明了输出结果的汉明重量与能量消耗之间有明确的关系，能量消耗随着汉明重量的增大而增大，而且有较为明确的界限，经过计算，它们的相关系数甚至能够达到0.9919[4]。这也说明CPA使用汉明重量模型是合理的。

3.2 CPA攻击方法

        由于字节替换占用了总能量消耗的大部分[5]，因此在CPA攻击时可以只考虑S-BOX的输出与能量迹之间的关系。

        本文将密钥分成16个子密钥分别破解，每一子密钥为一个字节。首先考虑第一个子密钥GuessKey的破解，这里需要将其从0遍历到255，然后每遍历一个值，就参照AES的一轮加密过程，将其与明文pt进行异或，异或之后再经过S-BOX的字节替换即可得到用于求解汉明重量的输入字符串input，如算法2第6行所示。值得注意的是AES加密需要对原始密钥进行密钥扩展，将一个原始密钥扩展成11个轮密钥，但是如算法2第4行所示，这里轮秘钥并不是密钥扩展得到的，而是直接对原始密钥进行了异或。这是因为，从本文2.1部分密钥扩展的过程可以看出，第一个轮密钥就是原始密钥本身，而且此处我们也只需要考虑AES的第一轮能量消耗和汉明重量之间的关系即可，因此在这里进行AES第一轮操作时可以不用进行密钥扩展而直接使用原始密钥。而后将输入字符串input的汉明重量求出，存在数组中，并求出他们与能量迹的Pearson相关系数。于是便可以得到横坐标为256个GuessKey，纵坐标为相关系数的统计图（请参看附件文件夹中的图），若遍历到的密钥不正确，则相关系数的波动幅度并不大，而当猜测的密钥正确时，对应的相关系数将会是一个明显的波峰。

算法2：CPA攻击算法
输入：能量迹traces，明文pt 输出：密钥keys 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
for i = 0; i<16 ;i++ do
    for GuessKey=0;GuessKey<256;GuessKey++ do
       for j = 0;j<TraceCnt;j++ do
             input=pt[j][i]⊕GuessKey;
             input=SubBytes(input);
             hws[j]=HammingWeight(input);
       end

       for j = 0;j<PointsCnt;j++ do
             pccs[j]=PCC(Trans(traces)[j],hws);
              /*PCC为求Pearson相关系数*/
              /*Trans为矩阵转置*/
       end

       CPA[GuessKey]=Max(pccs)
     end

     keys[i]=Argmax(CPA)
end

4 结论

        本次实验所得到的能量迹数据为第36组，攻击源代码可以参看source目录，先通过ReadFile.py读取实验数据,并将其转为攻击代码需要的格式。再执行CPA.py进行攻击，执行过程中通过matplolt画图，可以很清晰地看出相关系数峰值，这些图可以在附件文件夹中看到。最终测算出来的密钥为0x77 70 26 8a 51 bf a9 b2 2f 6f 40 69 c3 95 db 5b。使用source目录下的AES代码[6]加密明文，并将得到的密文与给定的密文进行对比，可确定其为正确的密钥。因此可以认为本攻击手段采用CPA攻击是合理的。

代码在此处下载

参考文献

[1] KOCHER P, JAFFE J, JUN B. Differential power analysis[C]//Annual
International Cryptology Conference. Springer, 1999: 388–397.

[2] BRIER E, CLAVIER C, OLIVIER F. Correlation Power Analysis with a Leakage
Model[G]//JOYE M, QUISQUATER J-J. Cryptographic Hardware and Embedded Systems -
CHES 2004. Berlin, Heidelberg: Springer Berlin Heidelberg, 2004, 3156: 16–29.

[3] DAEMEN J. The Rijndael Block Cipher[J]. : 45.

[4] LO O, BUCHANAN W J, CARSON D. Power analysis attacks on the AES-128 S-box
using differential power analysis (DPA) and correlation power analysis (CPA)[J].
Journal of Cyber Security Technology, 2017, 1(2): 88–107.

[5] MORIOKA S, SATOH A. An Optimized S-Box Circuit Architecture for Low Power
AES Design[G]//KALISKI B S, KOÇ çetin K, PAAR C. Cryptographic Hardware and
Embedded Systems - CHES 2002. Berlin, Heidelberg: Springer Berlin Heidelberg,
2003, 2523: 172–186.

[6] Skycker/AES: Rijndael cipher algorithm[EB/OL]. [2018-07-31].
https://github.com/Skycker/AES.

Posted on | In

        Spectre以及meltdown漏洞是前段时间，十分热门的两个漏洞，它们之所以广受重视，是因为它们根据的是体系结构的设计漏洞，而非针对某个系统或者某个软件，因此它几乎可以遍及大多数近代的CPU。

这里主要有三个漏洞:

  • Variant 1: bounds check bypass (CVE-2017-5753)【绕过边界检查】
  • Variant 2: branch target injection (CVE-2017-5715)【分支目标注入】
  • Variant 3: rogue data cache load (CVE-2017-5754)【恶意数据缓存载入】
    Spectre 主要利用前两个漏洞进行攻击，而meltdown则主要利用第三个漏洞进行攻击。

一、内存映射

        Linux和Windows的内存映射方法是不同的，在linux中，虚拟空间地址有4G，0~3G为用户空间，3~4G为内核空间
虚拟空间

其中内核空间都相同，准确的讲是每个进程共享同一个内核空间
虚拟内存

        Linux在启动时会初始化一个进程，然后通过fork()生成子进程，Linux的fork机制会把父进程的页表和堆栈等一模一样地复制一份，然后在运行时，子进程通过缺页异常等操作来改变用户空间，如果内核空间部分也改变了，则只修改初始化进程的内核空间，其它子进程访问该页时，再通过缺页中断将这部分内容从父进程更新过来。

        一般来讲，当进程进行系统调用进入内核态的时候，它应该能够访问整个地址空间的，但是在这里只能访问自己的1G的地址空间，于是我们需要通过地址的映射，来使他可以访问整个空间，内核空间分为：ZONE_DMA（内存开始的16MB） 、ZONE_NORMAL（16MB~896MB）、ZONE_HIGHMEM（896MB ~ 结束）三个区域，其中0~896M是直接映射的，其余部分会进行非线性映射。

这里写图片描述

二、Tomasulo算法

tomasylo

        原始的Tomasulo算法是为了寄存器重命名以便消除指令的数据相关，数据一到就可以执行指令。

  1. 指令首先存在于指令队列之中。
  2. 指令一条一条地从队列中取出来，进行译码，然后放到对应的操作保留站中，比如加法指令放到加法保留站中。乘法指令放到乘除法保留站中。Vj和Vk中是用来存储源操作数的（已经就绪的源操作数值取自于浮点寄存器），若源操作数还没有准备好，则通过Qj和Qk指向操作数的保留站号，等到被指向的保留站中的操作计算出了结果，则结果可以通过结果总线传回到保留站中需要的指令，然后将其Qj和Qk中的值改为0（表示已经准备好）。
  3. 当Qj和Qk都为0时，那一条指令就可以送到乘/除器中执行。

三、乱序执行

        最早期 CPU都是顺序执行的，前一条指令未执行完毕，则后一条指令必须等待着，就像我们烧水，必须洗茶壶，烧水，洗茶杯，倒水必须按照顺序来做，但是事实上烧水和洗茶杯可以同时执行，其实有很多指令也是如此，调整它们的顺序可以加快程序执行的速度

可能会造成乱序执行的原因：

  1. 编译器为了优化而实现指令重排（静态调度）
  2. CPU实现指令的多发射，以及并行执行，并为了优化实现指令的重排（动态调度）

        程序的乱序执行并不意味着在所有步骤中，指令的顺序都是混乱的，事实上，指令在发射时和提交时依然是顺序的，只是在执行的过程中会打乱顺序。

为了支持乱序执行
带有ROB的Tomasulo算法

        我们在Tomasulo 算法中加入了ROB来使得提交结果的时候能够按照顺序提交，执行的结果暂时存放于ROB而不直接写入寄存器堆，然后再按顺序提交数据。从而可以不出问题。

本次的漏洞就是利用了乱序执行这一特性来实现的

四、分支预测

由于在指令中存在许多跳转和分支，为了提前访问分支中的代码以节约时间，我们加入了分支预测功能

静态分支

对于所有的跳转指令，我们都预测执行跳转或者执行不跳转，则称其为静态跳转

动态分支

动态分支将会通过历史跳转信息来预测下一次分支应该选择跳转还是选择不跳转。在intel设计中有一个称为BTB(Branch Target Buffer)的部件，当我们执行分支指令时，会将执行结果和分支指令地址记录在其中，当下次取址时，查询其中的记录，若存在，则根据历史执行记录进行预测是否跳转。

若不存在此记录，我们将会使用静态分支预测器，我们一般将向上跳转的分支指令看作循环，对于循环我们倾向于接受跳转，而对于向下跳转，我们倾向于不跳转。

五、Meltdown攻击

这里写图片描述
        在第一行，我们引发了一个异常，若程序按照顺序执行，第三行的access将不会被执行，但是由于程序是乱序执行的，因此在异常引发之前，第三行的access将被执行，但是执行结果存在ROB中不会被提交，当异常触发以后，第三行的执行结果将被撤销掉，从计算机外部看来第三行的access就跟从未被执行过一样，但是事实上它只是在后期被撤销了，这会带来一个小问题，就是在执行过程中，刚才读取的数据已经被存储到高速缓存中。

我们可以通过侧信道攻击来确认刚才访问的数据是什么。

这里写图片描述
这段代码揭示了攻击的关键部分
首先我们将访问内核地址并取内容到寄存器内，
若这一举动可以触发异常，则对应的寄存器清零，若异常未处理，则应用程序将会被终止，并且取出的值将会存入应用程序核心转储的寄存器中。我们要做的就是通过第5行将相应的寄存器清零，从而可以判断这是一个错误的值。然后再次重试，直到遇到一个不为0的值，然后将秘密的值作为地址，去做读取操作，以便cache记录到这个地址，实现侧信道攻击。

六、Spectre

这里写图片描述
        Spectre主要利用了分支预测和乱序执行的漏洞实现的，如图所示的代码，看起来十分地正常，若x小于array1的长度的时候，循环顺利执行。但是我们假设这里有一个存储密码的变量地址为secret，并且令a=secret-array1，于是我们可以使用array1[a]来表示secret的值。当多次执行循环的时候，我们的x满足循环条件，则我们的分支预测模块会认为下一个循环也满足循环条件而去预执行这个循环，若此时我们将a的值赋值给x，则分支预测模块预测本次循环为执行（其实并不会执行），CPU会预执行这个循环体，然后将我们存储密码的secret值取出来，并将其作为地址去访问array2，但是最终发现循环不应该被执行，于是刚才取出来的值将会被作废。但是我们的这个secret值的地址已经被存入到缓存中去。我们最终可以将array2读取一遍，若读取某个地址的时候，访问的时间特别短，则说明这个地址就是那个被存入缓存的地址（即我们的密码值）。

七、参考

https://googleprojectzero.blogspot.co.at/2018/01/reading-privileged-memory-with-side.html

https://lwn.net/Articles/738975/

http://lib.csdn.net/article/linux/29085

https://bugs.chromium.org/p/project-zero/issues/detail?id=1272

http://blog.csdn.net/yiyeguzhou100/article/details/72875122

https://bbs.pediy.com/thread-61327.htm

http://blog.csdn.net/muxiqingyang/article/details/6686738

Posted on | In

一、背景

        由于计算核芯和电子商务的兴起，有必要在硬件层面保护我们的数据安全，目前面临的主要威胁是来自内存的攻击，包括时间和空间上两方面的侵入，团队制造出了一个名为Shakti-T的轻量级安全扩展芯片来解决这些问题，本处理器仅使用194个LUTs以及2197个触发器。

二、攻击类型

刚刚提到了基于内存的攻击

1. 基于空间上的攻击 -指针访问了它不允许被访问的地方。
   比较著名的例子有buffer-overflow，blaster-worm以及用于DDoS的slammer worm,安卓的Root也是利用了这个原理.
2. 基于时间上的攻击 -指针访问了已经被释放的地方。

三、解决方案

        前人对这两个问题提出了许多解决方案，为了解决问题一，有人提出了Lock and Key的方案，或者

- Stack Canaries,
- Encryption of The Code Pointer,
- Rearranging argument locations,
- 以及the Address Space Layout Randomization(ASLR)

等方法，而对于问题二，也有人提出富指针的方案，其中ASLR是抵御ROP(Return Oriented Programming)问题最好的方法，但是它依然存在一些问题，攻击者可以通过改变控制流的方法来绕过它们的检查。同时富指针方案也存在着高开销，缺乏稳定性等问题，即便有硬件层面的解决方案，当多个指针同时存在时也会失效。

四、富指针（Fat-Pointer）

        所谓富指针就是指，在原先指针的数据结构上再加上基地址和限长两个元素，每次为指针分配一个地址空间的时候，都会自动写入这块地址的起始位置和长度，而每次访问指针时，都会检查是否越界，以此来防止指针在释放后再次读取的问题.但是传统的方法有一个十分遗憾的问题，假如存在{P1，P2…..Pn}n个指针，它们同时指向同一个空间，当释放其中一个以后，由于是各存一份，访问其它指针依然会认为是正常访问，但实际上已经出现了空间上的攻击。

五、提出的方案

我们使用的是基于硬件的富指针:

  1. 基地址和边界统一存放于一个PLM（Pointer Limits Memory），而PLM的地址存于PLBR寄存器
  2. 每一个指针对应一个ptr_id
  3. 每次调用指针时使用ptr_id调取对应的基地址和边界，
    表格

我们使用如图表格来作为缓存，

  1. 其中左边的GPR（General Purpose Register）分两个部分一个是Tag bits，用于标记是数据还是指针，另一部分是寄存器的数值。
  2. 右边的BnBIndex和BnBLookUp包含在一个名为BnBCache的寄存器中，BnBIndex中的index表示BnBLookUp的位置，有效位V的值若为1，则表示可以从BnBLookUp中取到值，若为0，则说明需要从内存中去取所需的信息，当BnBLookUp中的信息被更新时，BnBindex中的信息也会被同步更新。BnBLookUp中的有效位V为1则表示它目前可用，为0则表示它可能被释放了。当BnBLookUp中的空间不足，则用LRU(最近最少使用)算法进行替换。

六、副作用及解决方案

        比如有的时候调用函数，某个寄存器被push了，若此时正好这个寄存器被替换出去，但是当数据再次被pop的时候那个寄存器已经是无效的了。于是需要新设计一个BnBStack（Base and Bound Stack）用于专门存放暂时被push的指针ptr_id.

七、结果

  1. 安全性：还是同样的问题，此处有（P1，P2….Pn）n个指针，若它们指向同一个地址，其中一个释放以后，BnBLookUp中有效位被置0，其它指针再访问它时，就可以得知它是无效的消息。
  2. 节约内存 :（P1，P2….Pn）n个指针,若他们指向同一个地址，则需要存n个ptr_id和1个base，一个bound，共n+2个空间。但传统的方法，每一个指针都需要存一份，则需要2n个空间。但如果这些指针分别指向不同的空间，则本方案更耗费一些空间。

William
会打代码的扫地王大爷
wlmnzf
中科院信工所
IIE
CAS
csuncle
丁洁的男朋友
丁洁的人
王立敏

Posted on | In

一、安装

1.1、组件安装

Windows 10中默认并没有安装子系统组件，我们需要安装它

控制面板->程序->程序与功能->启用和关闭Windows功能->勾选适用于Linux的Windows子系统Beta，确定即可安装。

1.2、开发者权限开启

设置->更新和安全->针对开发人员->选中 开发人员模式

1.3、安装

打开 命令提示符，输入bash进行安装，但是比较慢，建议挂载 V P N进行下载。

二、常见功能使用

Tips:如果你的Windows是正式版的，并没有通过快速更新到Windows秋季创意者版本，那么你的ubuntu版本是14.04版本的。

2.1、更换源

此处采用@littlemonsters的方法，将其更换为阿里云的源，否则不仅速度慢，而且有些源中的软件包版本实在是低下，会有很多问题比如Nodjs安装。

1
2
sudo cp /etc/apt/sources.list /etc/apt/sources.list.bak #备份
sudo vim /etc/apt/sources.list #修改

将阿里云的源复制进去

1
2
3
4
5
6
7
8
9
10
deb http://mirrors.aliyun.com/ubuntu/ trusty main restricted universe multiverse
deb http://mirrors.aliyun.com/ubuntu/ trusty-security main restricted universe multiverse
deb http://mirrors.aliyun.com/ubuntu/ trusty-updates main restricted universe multiverse
deb http://mirrors.aliyun.com/ubuntu/ trusty-proposed main restricted universe multiverse
deb http://mirrors.aliyun.com/ubuntu/ trusty-backports main restricted universe multiverse
deb-src http://mirrors.aliyun.com/ubuntu/ trusty main restricted universe multiverse
deb-src http://mirrors.aliyun.com/ubuntu/ trusty-security main restricted universe multiverse
deb-src http://mirrors.aliyun.com/ubuntu/ trusty-updates main restricted universe multiverse
deb-src http://mirrors.aliyun.com/ubuntu/ trusty-proposed main restricted universe multiverse
deb-src http://mirrors.aliyun.com/ubuntu/ trusty-backports main restricted universe multiverse

1
sudo apt-get update #更新列表

2.2、常见使用方法

2.2.1.启动

使用bash即可在当前目录启动linux

2.2.2.重装

有的时候linux被我们玩坏了，大环境结果全乱掉了，最好的办法就是重装

1
2
lxrun /uninstall    卸载linux子系统
lxrun /install        安装linux子系统

三、显示GUI

我们只有一个命令行，看起来就像连接服务器的shell，那万一我们需要运行我们的桌面窗口程序呢？国外大神们当然已经折腾除了方法。

3.1、安装VcXsrv

下载地址:https://sourceforge.net/projects/vcxsrv/

安装以后会有两个程序，分别是XLaunch和VcXsrv，它们可以用来远程访问linux。所以其实在这里就是利用它们来访问命令行内的linux。

3.2、Linux内安装桌面

1
2
3
sudo apt-get install ubuntu-desktop
sudo apt-get install unity
sudo apt-get install compizconfig-settings-manager

接着配置显示方式

1
2
3
cd ~
sudo vim .bashrc
把export DISPLAY=:0.0复制进去

3.3、配置compiz

  1. 打开刚才安装的XLaunch

  2. 命令行输入sudo ccsm进入显示界面，这里和后面的打开compiz建议用管理员权限，理论上不加管理员也可以，但是本人在使用过程中出了不少奇怪的问题。

  3. 如图所示勾选上需要安装的插件
    这里写图片描述

这里写图片描述
这里写图片描述

点击close关闭即可。

PS：如果遇到配置选项无法保存的情况，可尝试以下方法

  1. 安装compizconfig-backend-gconf

    1
    sudo apt-get install compizconfig-backend-gconf

  2. 进入CCSM->Preferences,将Backend改为Gsettings Configuration Backend，并且勾选Enable Intergration into the desktop environment

  3. 勾选插件，如果遇到冲突，则把冲突的插件关闭即可（确保上图的几个插件勾选，别的可以关闭，即可）

3.4、开启桌面

输入sudo compiz 不出意外的话即可在XLaunch上看到桌面的真正面目了。
这里写图片描述

这里如果不用sudo,在我这里就是不加载插件，也没有任何报错提示，就是这么吓人。

Posted on | In

PS:本文中的log等同于我们国内的ln

sigmoid函数

    之前那一文中提到了一般的梯度上升的公式推导，但是在《机器学习实战》一书中，实现的是分类方法，因此，虽然最终的结果相似，但是其实本质有很大的不同。

    一般来讲我们把实物分成两类，因此我们需要将结果映射到两个结果(是或非)，因为一般的阶跃函数在求导之类的问题上会变得相当复杂，因此我们用一个更加圆滑的sigmoid函数来映射，所有输入到这个函数的实数都会被转化到0-1之间，它的公式为 $ g(z)=\frac{1}{1+e^{-z}} $

    同时它对应的图像如图所示:
sigmoid

    于是我们可以将得到的结果进行四舍五入，分类成0或1

Logistic 回归

    这里的意思是，将我们的分类边界线作模型，进行拟合，并以此来分类。

     我们假设经过sigmoid函数处理过的结果为 $h_{\Theta}(x)$ ,因为是在0-1之间，因此可以看做是概率，另外，我们可以假设，分类到0或者1的概率。

$$
P(y=1|x;\theta)=h_{\theta}(x) \\
P(y=0|x;\theta)=1-h_{\theta}(x) \tag{1}
$$

将以上两个概率公式整合一下成为一个概率公式，

$$
p(y|x;\theta)=(h_\theta(x))^y(1-h_\theta(x))^{1-y} \tag{2} \\
$$

梯度上升解决回归问题

1. 最大似然估计

     这里我们使用最大似然估计法，这个在大学的高等数学中应该都有学习过，就不在赘述。这里假设我们有m个训练集。

$$
L( \theta )=\prod_{i=1}^{m}p(y^{(i)}|x^{(i)};\theta)=\prod_{i=1}^{m}(h_\theta(x^{(i)}))^{y^{(i)}}(1-h_\theta(x^{(i)}))^{1-{y^{(i)}}} \tag{3}
$$

     为了求导方便，我们一般会将似然函数L加上log函数，因为log函数是递增函数，因此不影响似然函数求最值。
这里会用到一个log函数的性质 $log a^b=b log a$ ，推导得：

$$
l(\theta)=logL(\theta)=\sum_{i=1}^my^{(i)}logh(x^{(i)})+(1-y^{(i)})log(1-h(x^{(i)})) \tag{4}
$$

     将l函数对$\theta$求导

$$
\frac{\partial}{\partial\theta_j }l(\theta)=(y\frac{1}{h_\theta (x)}-(1-y)\frac{1}{1-h_\theta (x)})\frac{\partial}{\partial\theta_j}h_\theta x \tag{5}
$$

2. sigmoid函数求导

$$
\begin{equation}
\begin{split}
&h’(x)=\frac{d}{dx}\frac{1}{1+e^{-x}}\\
&=\frac{1}{(1+e^{-x})^2} (e^{-x})\\
&=\frac{1}{(1+e^{-x})}(1-\frac{1}{(1+e^{-x})})\\
&=h(x)(1-h(x))
\end{split}
\end{equation} \tag{6}
$$

3. 似然估计后续

     从上一篇文章，或者从《机器学习实战》chapter5 中可得sigmoid函数h(x)的输入函数是$w=\theta^Tx$,将其代入公式(4)，得到

$$
\begin{equation}
\begin{split}
&l’(\theta)=(y\frac{1}{h(\theta^Tx)}-(1-y)\frac{1}{1-h{(\theta^Tx)}}) \frac{\partial}{\partial\theta_j}h(\theta^Tx)\\
&=(\frac{1}{h(\theta^Tx)}-(1-y)\frac{1}{1-h(\theta^Tx)})h(\theta^Tx)(1-h(\theta^Tx)\frac{\partial}{\partial_j}\theta^Tx)\\
&=(y(1-h(\theta^Tx))-(1-y)h(\theta^T x))x_j\\
&=(y-h_\theta(x))x_j
\end{split}
\end{equation} \tag{7}
$$


William
会打代码的扫地王大爷
wlmnzf
中科院信工所
IIE
CAS
csuncle
丁洁的男朋友
丁洁的人
王立敏

Posted on | In

前言

    本来对数学没什么感觉的，但是停摆了一年复习考研，于是开始对数学有些感觉了，之前看到《机器学习实战》中第五章中梯度上升法，使用了一个它所谓的十分简单的推导，一直好奇怎么个简单法，于是重新学习机器学习的相关算法，这次将主推数学推导。

有监督回归算法

    在机器学习中，多元线性回归模型是经常使用的模型，比如在吴恩达《斯坦福机器学习》中的例子，我们需要根据已有的房价信息预测当前房子的房价，于是我们收集到一些房价数据。

房价信息

    再将它们画在二维坐标上，它们就以离散的点分布在平面上，如下所示
房价分布情况

    我们希望能根据这些已知的点来预测我们想知道的房子的房价，因此我们需要找到一条规律，也就是一条大致经过这些点的线性模型，在数学上我们通常称之为拟合，而这个拟合的过程，我们称之为回归。

拟合结果

    假设我们建立的模型是一元一次的，将得到这样的拟合结果，于是我们可以x轴上的房屋面积，找到对应的房屋价格。

    有监督的学习算法，可以理解成我们训练模型的时候每一个输入都是有标准答案的，我们通过预测值跟标准答案的比对，不断修改模型的参数才能最终实现较好地的拟合结果。

最小二乘法

    最小二乘法是我们经常使用的拟合算法，它通过最小化误差的平方和寻找数据的最佳函数匹配。

    以我们《机器学习实战》第五章作例子，我们假设的模型为z，于是函数即可设为

$$
\begin{equation}
z=w0+w_1x_1+w2x2+w3x3+….+w_nx_n\\=w_0x_0+w_1x_1+w2x2+w3x3+….+w_nx_n (x0=1) \tag{1}
\end{equation}
$$

    这种写法也可以表示为向量的写法:

$$
z=w^Tx=
\begin{bmatrix}
w_0&w_1&…&w_n
\end{bmatrix}
\begin{bmatrix}
x_0\\
x_1\\
…\\
x_n\\
\end{bmatrix} \tag{2}
$$

    同样的道理，我们也可以这样子表示

$$
z=x^Tw=
\begin{bmatrix}
x_0&x_1&…&x_n
\end{bmatrix}
\begin{bmatrix}
w_0\\
w_1\\
…\\
w_n\\
\end{bmatrix} \tag{3}
$$

    刚才我们也提到了，最小二乘法拟合的原理是最小化误差的平方和，我们将这个平方和称为损失函数，跟我们平时常用的方差类似，当这个损失函数越小，我们的模型就越能跟离散的点匹配起来:

$$
f(w)=\frac{1}{2} \sum_{i=1}^m(z_w( x_i) -y_j )^2 \tag{4}
$$

其中的y表示我们给出的标准的特征 $
\begin{bmatrix}
y_0\\
y_1\\
…\\
y_m\\
\end{bmatrix}
$

    因为梯度上升算法是用来计算函数的最大值的，而梯度下降算法则是计算函数最小值的。而我们的损失函数自然是越小越好，我们需要求得一个系数来使得f(w)最小，可是使用梯度上升法是用于求最大值的，因此为了用上梯度上升算法，我们最终应该在f(w)前加上负号。假设:

$$
J(w)=-f(w) \tag{5}
$$

接下来我们开始利用矩阵来推算我们的数学公式，因为原始的公式用来做迭代计算会很不方便，因此我们需要一个等价的公式来让我们的算法更加高效，就例如《机器学习实战》chapter5中的那样。假设我们的输入为X,我们有m组训练数据，每个数据有n个特征。则:

$$
\begin{equation}
X=
\begin{bmatrix}
x_{11}&x_{12}&…&x_{1n}\\
x_{21}&x_{22}&…&x_{2n}\\
…&…&…&…\\
x_{m1}&x_{m2}&…&x_{mn}\
\end{bmatrix}
=
\begin{bmatrix}
x_1^{T}\\
x_2 ^{T}\\
…\\
x_m\\
\end{bmatrix} \tag{6}
\end{equation}
$$

于是通过（3）可以推出

$$
Xw=
\begin{bmatrix}
x_1^T\\
x_2^T\\
…\\
x_m^T\\
\end{bmatrix}
w=
\begin{bmatrix}
x_1^Tw\\
x_2^Tw\\
…\\
x_m^Tw\\
\end{bmatrix}=
\begin{bmatrix}
z_w(x_1)\\
z_w(x_2)\\
…\\
z_w(x_m)\\
\end{bmatrix} \tag{7}
$$

$$
Xw-\overrightarrow{y}=
\begin{bmatrix}
x_1^Tw\\
x_2^Tw\\
…\\
x_m^Tw\\
\end{bmatrix}-
\begin{bmatrix}
y_1\\
y_2\\
…\\
y_m\\
\end{bmatrix}=
\begin{bmatrix}
z_w(x_1)-y_1\\
z_w(x_2)-y_2\\
…\\
z_w(x_m)-y_m
\end{bmatrix} \tag{8}
$$

由矩阵内积可得

$$
\because z^Tz=\sum_i^nz_i^2 \tag{9}
$$

$$
\therefore \frac{1}{2}(Xw-\overrightarrow{y})^T(Xw-\overrightarrow{y})= \frac{1}{2}\sum_{i=1}^n(z_w(x_i)-y_i)^2=f(w) \tag{10}
$$

则梯度为

$$
\begin{equation}
\begin{split}
&\nabla_wf(w)=\nabla_w\frac{1}{2}(Xw-\overrightarrow{y})^T(Xw-\overrightarrow{y})\\
&=\frac{1}{2}\nabla_w(w^TX^TXw-w^TX^T\overrightarrow{y}-\overrightarrow{y}^TXw+\overrightarrow{y}^T\overrightarrow{y})\\
&=\frac{1}{2}\nabla_wtr(w^TX^TXw-w^TX^T\overrightarrow{y}-\overrightarrow{y}^TXw+\overrightarrow{y}^T\overrightarrow{y}) \\
&=\frac{1}{2}\nabla_w(trw^TX^TXw-2tr\overrightarrow{y}^TXw) \\
&=\frac{1}{2}(X^TXw+X^TXw-2X^T\overrightarrow{y})\\
&=X^TXw-X^T\overrightarrow{y}=X^T(Xw-\overrightarrow{y})\\\\
&=>J(w)=-f(w)=X^T(\overrightarrow{y}-Xw)
\end{split}
\end{equation} \tag{11}
$$

说明：
第二步：类似于括号展开
第三步:实数的迹等于它本身
第四步:因为 $\overrightarrow{y}^T\overrightarrow{y}$ 不含w，因此它对w求导为0.并且利用了公式 $trA=trA^T$ 进行简化。
第五步:利用公式 $\nabla_{A^T}trABA^TC=B^TA^TC^T+BA^TC$ ,令 $A^T=w,B=B^T=X^TX,C=I$ ,利用公式转化即可得到。

最后再回到《机器学习实战》中，P78,代码清单5-1②的部分。
dataMatrix=X;
weights=w;
labelMat=y;
把等号右边的用左边的变量代入，不过很遗憾，还是有些区别的，在《机器学习实战》一书中，还有sigmoid这一函数，查阅了一些资料，发现其实还是有些区别的，将于下一篇博文中阐明。

参考

吴恩达《机器学习》notes1
周志华《机器学习》chapter3 线性模型

来源

http://csuncle.com/2017/06/13/《机器学习实战》-chapter5梯度上升算法-数学推导/